2．古书说：“国之大事，在祀在戎”。从下面的几幅青铜器皿图片可以看出，当时我国的青铜器主要属于：

A．农具和酒器　　 B．礼器和兵器　　 C．礼器和用具　　 D．兵器和农具

1．《史记•秦始皇本纪》载：秦始皇二十六年(前 221)下令“更名民曰黔首”。秦始皇三十一年(前227)下令“使黔首自实田”。黔首之称，在战国时已经广泛使用，含义与当时常见的“民”、“庶民”相同。下列选项中同属于对百姓称呼的是①黎庶　 ②苍生　 ③优伶　 ④氓 　　 A.①②④　　　 B.②③④　　　 C.①③④　　　 D.①②③④

6．棱柱的何两个平面都可以作为棱柱的底面吗？

5．有两个面互相平行，其余后面都是平行四边形的几何体是不是棱柱(举反例说明，如图)

4.正四棱锥的底面积为46 cm²,侧面等腰三角形面积为6 cm²,求正四棱锥侧棱.

3.已知圆柱的底面半径为3cm,,轴截面面积为24 cm²,求圆柱的母线长.

2. 已知圆锥的轴截面等腰三角形的腰长为 5cm,,面积为12 cm²,求圆锥的底面半径.

3. 小结：几何图形；相关概念；相关性质；生活实例

2. 教学圆柱、圆锥的结构特征：

① 讨论：圆柱、圆锥如何形成？

② 定义：以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体叫圆柱；以直角三角形的一条直角边为旋转轴,其余两边旋转所成的曲面所围成的几何体叫圆锥.

　 → 列举生活中的棱柱实例　 →结合图形认识：底面、轴、侧面、母线、高. → 表示方法

③ 讨论：棱柱与圆柱、棱柱与棱锥的共同特征？ 　→ 柱体、锥体.

④ 观察书P2若干图形，找出相应几何体； 举例：生活中的柱体、锥体.

1. 教学棱柱、棱锥的结构特征：

① 提问：举例生活中有哪些实例给我们以两个面平行的形象？　

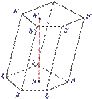② 讨论：给一个长方体模型，经过上、下两个底面用刀垂直切，得到的几何体有哪些公共特征？把这些几何体用水平力推斜后，仍然有哪些公共特征？

③ 定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫棱柱.

　→ 列举生活中的棱柱实例(三棱镜、方砖、六角螺帽).

　 结合图形认识：底面、侧面、侧棱、顶点、高、对角面、对角线.

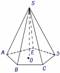④ 分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等.

　 表示：棱柱ABCDE-A’B’C’D’E’

⑤ 讨论：埃及金字塔具有什么几何特征？

⑥ 定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体叫棱锥.

结合图形认识：底面、侧面、侧棱、顶点、高. → 讨论：棱锥如何分类及表示？

⑦ 讨论：棱柱、棱锥分别具有一些什么几何性质？有什么共同的性质？

棱柱：两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形

棱锥：侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方.