
7.已知点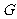 是△
是△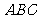 的重心,若
的重心,若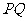 过△
过△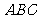 的重心
的重心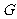 ,且
,且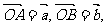
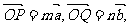 则
则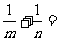
6.设平面向量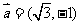 ,
,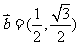 .若存在实数
.若存在实数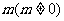 和角
和角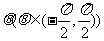 ,
,
使向量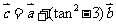 ,
,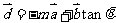 ,且
,且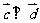 ,则函数
,则函数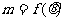 的关系式
的关系式
5.已知向量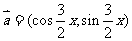 ,
,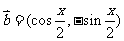 ,且
,且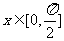
则函数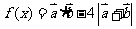 的最小值
的最小值
4.已知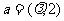 ,
,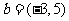 ,且
,且 与
与 的夹角为钝角,则
的夹角为钝角,则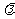 的取值范围是
的取值范围是
3.已知向量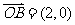 ,向量
,向量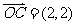 ,向量
,向量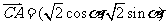 ,则向量
,则向量
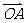 与向量
与向量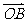 的夹角的取值范围是
的夹角的取值范围是
2.我们把平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为斜坐标系.平面上任意一点P的斜坐标定义为:若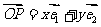 (其中
(其中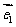 、
、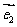 分别为斜坐标系的x轴、y轴正方向上的单位向量,x、y∈R),则点P的斜坐标为(x, y).在平面斜坐标系xoy中,若
分别为斜坐标系的x轴、y轴正方向上的单位向量,x、y∈R),则点P的斜坐标为(x, y).在平面斜坐标系xoy中,若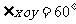 ,已知点M的斜坐标为 (1, 2),则点M到原点O的距离为
.
,已知点M的斜坐标为 (1, 2),则点M到原点O的距离为
.
1.已知两个向量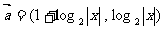 ,
,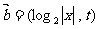
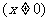 .若t=1且
.若t=1且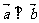 ,实数
,实数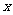 =
=
10.[解析]从表格中的数据我们可以看出当x增加10时,对应y的值减小100,所以y与x之间可能是一次函数的关系,我们可以根据图象发现这些点在一条直线上,所以y与x之间是一次函数的关系,然后设出一次函数关系式,求出其关系式.
[答案](1)画图如图;
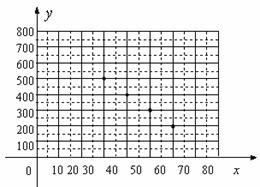
由图可猜想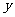 与
与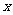 是一次函数关系,
是一次函数关系,
设这个一次函数为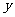 =
= 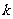
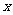 +
+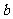 (k≠0)
(k≠0)
∵这个一次函数的图象经过(30,500)、(40,400)这两点,
∴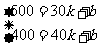 解得
解得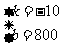
∴函数关系式是: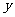 =-10
=-10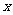 +800
+800
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得
W=(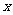 -20)(-10
-20)(-10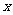 +800)=-10
+800)=-10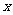
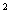 +1000
+1000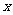 -16000
-16000
=-10(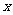 -50)
-50)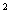 +9000
+9000
∴当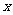 =50时,W有最大值9000.
=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元.
(3)对于函数 W=-10(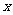 -50)
-50)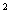 +9000,
+9000,
当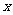 ≤45时,W的值随着x值的增大而增大,销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.
≤45时,W的值随着x值的增大而增大,销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.
9.[解析]观察分数的排列发现其分布有轴对称性,且(n,1)表示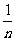 ,(n,2)表示
,(n,2)表示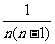
[答案]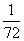
8.[解析]寻求图形与图形之间数字蕴含的规律是解题的关键所在.图形的第一行的数是连续正奇数;第二行左边的数是连续正偶数;把每个图形第一行的数乘以第二行左边的数,再加上第一行的数,便得到第二行右边的数.
[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com