
4.设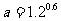 ,
,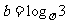 ,
,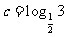 ,则有( )
,则有( )
A.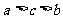 B.
B.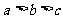 C.
C.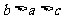 D.
D.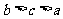
3.已知等差数列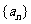 的前
的前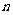 项和为
项和为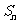 ,若
,若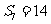 ,则
,则 的值为( )
的值为( )
A. 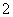 B.
B. 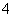 C.
C. 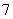 D.
D. 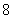
2.函数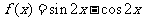 的最小正周期是( )
的最小正周期是( )
A.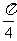 B.
B.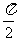 C.
C.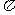 D.2
D.2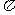
1.若集合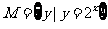 ,
,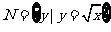 ,则
,则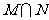 等于( )
等于( )
A. 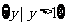 B.
B. 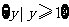 C.
C. 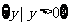 D.
D. 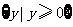
20.已知函数f(x)=a1x+a2x2+…+anxn(n∈N*),且a1,a2,a3,…,an构成数列{an},又f(1)=n2.
(1)求数列{an}的通项公式;
(2)求证: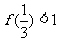 .
.
19.某地今年年初有居民住房面积为a m2,其中需要拆除的旧房面积占了一半.当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除x m2的旧住房,又知该地区人口年增长率为4.9‰.
(1)如果10年后该地的人均住房面积正好比目前翻一番,那么每年应拆除的旧住房面积x是多少?
(2)依照(1)拆房速度,共需多少年能拆除所有需要拆除的旧住房?
下列数据供计算时参考:
|
1.19=2.38 |
1.00499=1.04 |
|
1.110=2.60 |
1.004910=1.05 |
|
1.111=2.85 |
1.004911=1.06 |
18.设正项数列{an}的前n项和为Sn,且存在正数t,使得对所有正整数n,t与an的等差中项和t与Sn的等比中项相等,求证数列{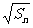 }为等差数列,并求{an}通项公式及前n项和.
}为等差数列,并求{an}通项公式及前n项和.
17.设首项为正数的等比数列,它的前n项和为80,前2n项的为6560,且前n项中数值最大的项为54,求此数列的首项和公比.
16.已知等差数列{an}的前项和为Sn,且S13>S6>S14,a2=24.
(1)求公差d的取值范围;(2)问数列{Sn}是否成存在最大项,若存在求,出最大时的n,若不存在,请说明理由.
15.设{an}为等差数列,{bn}为等比数列,且a1=b1=1,a2+a4=b3,b2b4=a3分别求出{an}及{bn}的前10项的和S10及T10.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com