
19.(本小题满分12分)盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球,规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得–1分.现从盒中任取3个球,(Ⅰ)求取出的3个球颜色互不相同的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设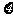 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求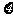 的分布列和数学期望.
的分布列和数学期望.
18.(本小题满分12分)有一个4×5×6的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成120个1×1×1的小正方体,从这些小正方体中随机地任取1个.
(Ⅰ)设小正方体涂上颜色的面数为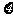 ,求
,求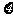 的分布列和数学期望.
的分布列和数学期望.
(Ⅱ)如每次从中任取一个小正方体,确定涂色的面数后,再放回,连续抽取6次,设恰好取到两面涂有颜色的小正方体次数为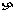 . 求
. 求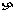 的数学期望.
的数学期望.
17.(本小题满分10分)甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为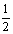 ,乙投篮命中的概率为
,乙投篮命中的概率为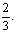
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.
16.函数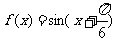 的图象按向量
的图象按向量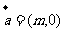 平移后得到
平移后得到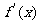 的图象,其中
的图象,其中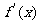 为
为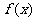 的导函数,且
的导函数,且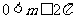 ,则
,则 .
.
15.利用数学归纳法证明(n+1)(n+2)…(n+n)=2n·1·3·…·(2n-1)时,由k到k+1左边应添加的因式是 .
14.设等差数列{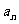 },{
},{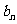 }的前
}的前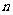 项的和分别为
项的和分别为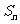 与
与 ,若
,若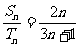 ,则
,则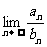 =
.
=
.
13.设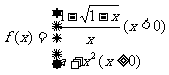 ,要使函数
,要使函数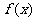 在
在 内连续,则
内连续,则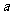 的值为
.
的值为
.
12. 设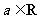 ,函数
,函数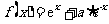 的导函数是
的导函数是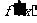 ,且
,且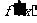 是奇函数,若曲线
是奇函数,若曲线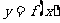 的一切线斜率是
的一切线斜率是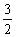 ,则切点的横坐标为
,则切点的横坐标为
A. 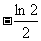 B.
B.
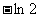 C.
C.
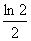 D.
D.
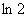
11.下列四个命题中,不正确的是
A.若函数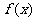 在
在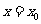 处连续,则
处连续,则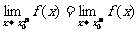

B.若函数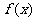 、
、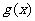 满足
满足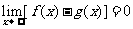 ,则
,则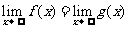

C.函数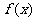 =
=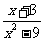 的不连续点是
的不连续点是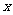 =3和
=3和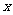 =-3
=-3
D.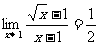

10.利用标准正态分布表我们可以求出一般正态总体在某一区间上取值的概率,若正态总体为N(1,9),则该正态分布在区间(1,10)上的概率为 
A. B.
B.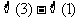 C.
C. D.
D.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com