
3. 1个氢原子由1个质子和1个电子构成,不含中子。当1个氢原子失去1个电子后,它不会变成( )
A. 质子 B. 原子核 C. 阳离子 D. 带负电荷的离子
2. 当原子的最外层电子数发生改变时,会引起改变的是( )
A. 相对原子质量 B. 元素种类 C. 中子数 D. 化学性质
1. 能保持物质化学性质的粒子是( )
A. 分子 B. 质子 C. 中子 D. 电子
3. 应用:根据粒子示意图判断阴阳离子和原子,化合价,化学式
① 原子:质子数=核外电子数;阴离子:质子数<核外电子数;阳离子:质子数>核外电子数
② 化合价是元素的性质;单质的化合价为零;离子化合物和共价化合物化合价原理不同
离子化合物中化合价与得失电子有关,得电子为负,失电子为正,数目与得失电子数目相同;
共价化合物中化合价与共用电子对有关,偏向为负,偏离为正,数目与共用电子对数目有关;
化合价规则:化合物中,元素正负化合价的代数和为零。
③ 在写化学式的同时,特别要注意化合价与元素符号的下表是否匹配
典型习题:
2. 了解:分子、原子、离子、元素的概念、区别、联系;原子的构成;相对原子(分子)质量
① 分子、原子、离子都是构成物质的粒子。
分子构成的物质:共价化合物(如:水、酒精、二氧化碳等);大部分非金属单质(如:氢气、氧气、氮气、硫等)
原子构成的物质:金刚石、石墨、单晶硅;稀有气体;金属单质
离子构成的物质:离子化合物(如氯化钠、氢氧化钙等)
注:(1)单一的离子是不能够形成物质的。例如:氯化钠是由氯离子与钠离子形成的,千万不能说是由氯化钠离子形成的
(2)离子化合物是通过阴阳离子相互吸引而形成的,共价化合物是通过共用电子对形成的
(3)判断方法:由金属元素(或铵根)与非金属元素形成的化合物都是离子化合物,完全由非金属元素形成的化合物是共价化合物
简单的判别方法:看其化合物的名称中是否有“钅”字旁,如有则是离子化合物,没有则是共价化合物
② 原子是由质子、中子、电子构成的,但并不是所有的原子中都含有三种粒子(如:氢原子中没有中子)
③ 相对原子质量=质子数+中子数(仅是数值关系)
相对分子质量=Σ(各原子相对原子质量)
④ 分子、原子、离子为微观概念;物质、元素为宏观概念
在做选择题、填空题中应注意概念的微观宏观匹配性
主要考点:
1. 常识:核外电子排布,原子结构示意图,原子团的概念
① 核外电子的分层排布,能量低的靠近原子核;第一层(K层)最多排2个电子,第二层(L层)最多排8个电子,最外层最多排8个电子;先排满内层,在排外层;
原子团在化学变化中,有可能改变
② 硝酸根离子NO3-;氯酸根离子ClO3-;氢氧根离子OH-;碳酸氢根离子HCO3-;碳酸根离子CO32-;硫酸根离子SO42-;锰酸根离子MnO42-;高锰酸根离子MnO4-;磷酸根离子PO43-;铵根离子NH4+
③ 注意原子结构示意图与离子结构示意图之间的区别:判断元素种类,根据核内质子数;判断是离子还是原子,根据核外电子总数与核内质子数
④ 地壳中含量前四位:氧(O)硅(Si)铝(Al)铁(Fe);空气中含量最多的元素:氮(N);海洋中含量最多的元素:氧(O)
⑤ 原子的最外层的电子数决定了:元素的化学性质,元素的分类,元素的化合价
证明:设公差为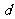 ,则
,则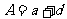
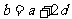
∴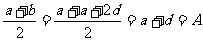
例四
《教学与测试》P77 例一:在-1与7之间顺次插入三个数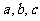 使这五个数成AP,求此数列。
使这五个数成AP,求此数列。
解一:∵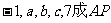 ∴
∴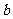 是-1与7 的等差中项
是-1与7 的等差中项
∴ 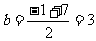
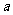 又是-1与3的等差中项 ∴
又是-1与3的等差中项 ∴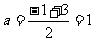
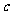 又是1与7的等差中项 ∴
又是1与7的等差中项 ∴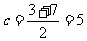
解二:设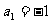
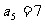 ∴
∴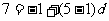
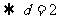
∴所求的数列为-1,1,3,5,7
出另一个。
3.寻求等差数列的通项公式:

由此归纳为 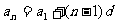 当
当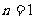 时
时 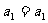 (成立)
(成立)
注意: 1° 等差数列的通项公式是关于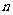 的一次函数
的一次函数
2° 如果通项公式是关于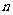 的一次函数,则该数列成AP
的一次函数,则该数列成AP
证明:若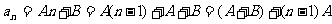
它是以 为首项,
为首项, 为公差的AP。
为公差的AP。
3° 公式中若 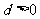 则数列递增,
则数列递增,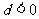 则数列递减
则数列递减
4° 图象: 一条直线上的一群孤立点
2.若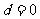 则该数列为常数列
则该数列为常数列
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com