
2.已知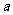 ,b都是实数,那么“
,b都是实数,那么“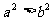 ”是“
”是“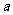 >b”的
( )
>b”的
( )
(A)充分而不必要条件
(B)必要而不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
1.已知U=R,A=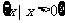 ,B=
,B=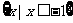 ,则
,则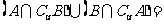 ( )
( )
(A)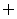 (B)
(B)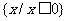 (C)
(C)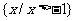 (D)
(D)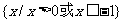

10.已知函数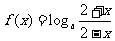
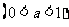
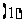 试判断
试判断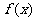 的奇偶性;
的奇偶性;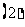 解不等式
解不等式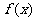 ≥
≥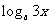
9.(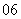 辽宁文)方程
辽宁文)方程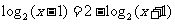 的解为
的解为
热点考向一:对数的化简与求值
例1:(1)化简: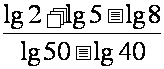
(2)化简;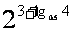
例2:求下列函数的值域 :
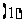
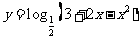 ;
; 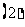
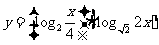 (
(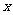 ≥
≥ )
)
例3 不等式
不等式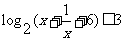 的解集为
的解集为
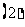 若不等式
若不等式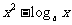 ≤
≤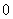 在
在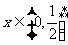 内恒成立,则
内恒成立,则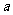 的取值范围是( )
的取值范围是( )
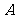
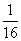 ≤
≤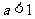
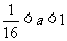
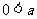 ≤
≤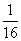
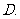
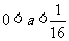
热点考向二:比大小
例4(1)已知函数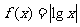 ,若
,若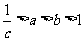 ,则
,则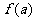 、
、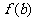 、
、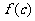 从小到大依次为
从小到大依次为
(2)设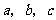 均为正数,且
均为正数,且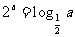 ,
,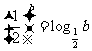 ,
,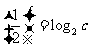 .则
.则
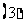 若
若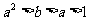 ,则
,则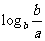 ,
,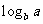 ,
,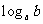 从小到大依次为
从小到大依次为
(4)已知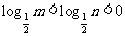 ,则( )
,则( )
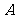
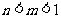
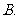
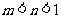
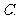
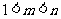
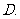
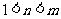
热点考向三:对数函数的性质的应用
例5:(1)设函数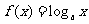 在区间
在区间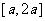 上的最大值与最小值之差为
上的最大值与最小值之差为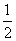 ,求a的值
,求a的值
(2)若函数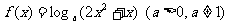 在区间
在区间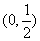 内恒有
内恒有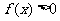 ,求
,求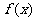 的单调递增区间
的单调递增区间
例6: 设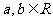 且
且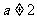 ,定义在区间
,定义在区间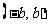 内的函数
内的函数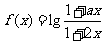 是奇函数.
是奇函数.
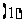 求
求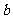 的取值范围;
的取值范围;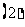 讨论函数
讨论函数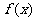 的单调性.
的单调性.
五当堂检测
 函数
函数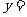
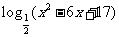 的值域是
的值域是
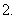 若定义在区间
若定义在区间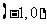 内的函数
内的函数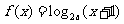 满足
满足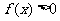 ,则
,则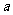 的
的
取值范围是
3.若函数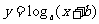
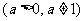 的图象过两点
的图象过两点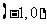 和
和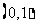 ,则 a
,则 a
= , b=
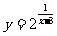 的值域为
;
的值域为
;
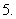
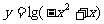 的递增区间为
,值域为
的递增区间为
,值域为
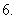
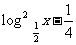 ≤
≤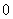 ,则
,则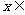
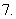 函数
函数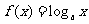
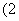 ≤
≤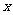 ≤
≤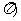 的最大值比最小值大
的最大值比最小值大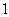 ,则
,则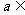
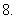 已知
已知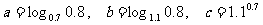 ,则
,则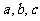 的大小关系是
的大小关系是
4.(08重庆)已知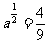 (a>0) ,则
(a>0) ,则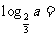
1(09北京理)为了得到函数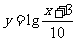 的图像,只需把函数
的图像,只需把函数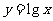 的图像上所有的点
( )A.向左平移3个单位长度,再向上平移1个单位长度
的图像上所有的点
( )A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
2(09全国理)设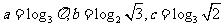 ,则 (( )
,则 (( )
A. 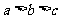 B.
B. 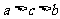 C.
C.
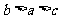 D.
D.
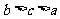
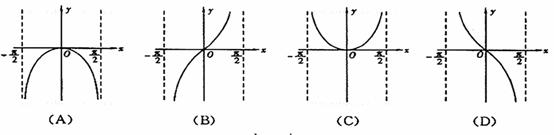
3.(08山东卷)函数y=lncosx(-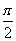 <x<
<x<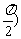 的图象是( )
的图象是( )
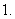 对数函数的概念、图象和性质:
对数函数的概念、图象和性质:
①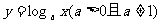 的定义域为
的定义域为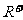 ,值域为
,值域为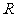 ;
;
②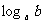 的符号规律:同范围时值为正,异范围时值为负。
的符号规律:同范围时值为正,异范围时值为负。
③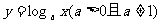 的单调性:
的单调性:
 时,在
时,在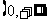 单增,
单增,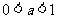 时,在
时,在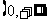 单减。
单减。
④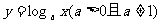 的图象特征:
的图象特征:
 时,图象像一撇,过
时,图象像一撇,过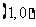 点,在
点,在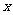 轴上方
轴上方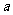 越大越靠近
越大越靠近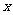 轴;
轴;
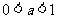 时,图象像一捺,过
时,图象像一捺,过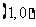 点,在
点,在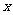 轴上方
轴上方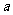 越小越靠近
越小越靠近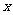 轴。
轴。
⑤“同正异负“法则:给定两个区间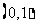 和
和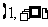 ,若
,若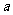 与
与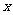 的范围处于同一个区间,则对数值大于零;否则若
的范围处于同一个区间,则对数值大于零;否则若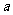 与
与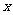 的范围分处两个区间,则对数值小于零.
的范围分处两个区间,则对数值小于零.
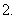 指数函数
指数函数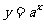 与对数函数
与对数函数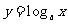 图像关于y=x对称;
图像关于y=x对称;
主要方法:
 解决与对数函数有关的问题,要特别重视定义域;
解决与对数函数有关的问题,要特别重视定义域;
 解决对数不等式、对数方程时,要重视考虑对数的真数、底数的范围;
解决对数不等式、对数方程时,要重视考虑对数的真数、底数的范围;
 对数不等式的主要解决思想是对数函数的单调性。
对数不等式的主要解决思想是对数函数的单调性。
热点提示:1.对数函数在高考中重点考查的是它的图像、性质及其简单应用,同时考查数学思想方法,以考查分类讨论及运算能力为主
2.以小题的形式考查对数函数的图像、性质,也可能与其他知识结合,以解答题出现,属中低档题
本节重点:运用对数函数的图象、性质解题.
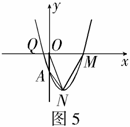
9.已知抛物线 经过点
经过点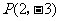 ,
,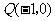 .
.
(1)求抛物线的解析式.
(2)设抛物线顶点为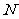 (如图5),与y轴交点为A.求
(如图5),与y轴交点为A.求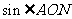 的值.
的值.
(3)设抛物线与x轴的另一个交点为M,求四边形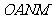 的面积.
的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com