
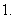 已知
已知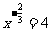 ,则
,则
 求
求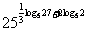 的值.
的值.
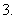 设
设 ,求
,求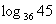 .
.
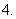 若
若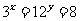 ,则
,则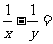
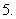 (
(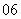 成都市诊断)
成都市诊断) 的值为
的值为 

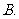
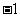
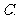
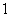
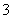
问题1.计算:
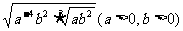 ;
;
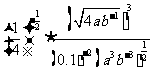
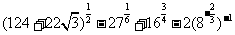
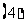
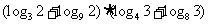 ;
;
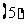
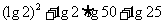 ;
;
问题2. 已知
已知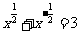 ,求
,求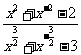 的值;
的值;
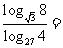

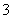
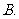
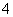
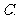
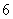
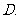
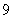
 已知
已知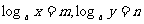 ,求
,求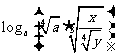 ;
;
问题3.已知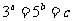 ,且
,且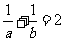 ,求
,求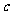 的值.
的值.
问题4. (
(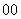 上海春)方程
上海春)方程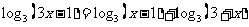 的解是
的解是
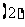 (
(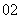 上海)方程
上海)方程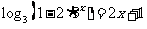 的解
的解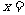
问题5.设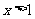 ,
,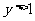 ,且
,且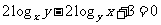 ,求
,求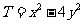 的最小值.
的最小值.
 重视指数式与对数式的互化;
重视指数式与对数式的互化;
 根式运算时,常转化为分数指数幂,再按幂的运算法则运算;
根式运算时,常转化为分数指数幂,再按幂的运算法则运算;
 不同底的对数运算问题,应化为同底对数式进行运算;
不同底的对数运算问题,应化为同底对数式进行运算;
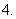 运用指数、对数的运算公式解题时,要注意公式成立的前提.
运用指数、对数的运算公式解题时,要注意公式成立的前提.
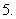 指数方程和对数方程按照不同类型的对应方法解决.
指数方程和对数方程按照不同类型的对应方法解决.
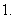
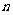 次方根的定义及性质:
次方根的定义及性质: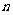 为奇数时,
为奇数时,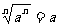 ,
,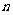 为偶数时,
为偶数时,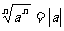 .
.
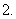 分数指数幂与根式的互化:
分数指数幂与根式的互化: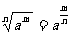 ,
,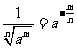 (
(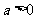 ,
, ,且
,且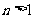 )
)
零的正分数指数幂为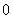 ,
,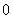 的负分数指数幂没有意义.
的负分数指数幂没有意义.
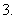 指数的运算性质:
指数的运算性质: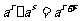 ,
,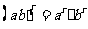 (其中
(其中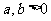 ,
,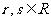 )
)
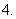 指数式与对数式的互化:
指数式与对数式的互化: .
.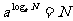 ,
,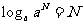 .
.
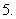 对数的运算法则:如果
对数的运算法则:如果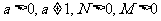 有
有
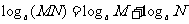 ;
; 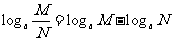 ;
;
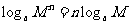 ;
;
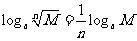
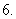 换底公式及换底性质:
换底公式及换底性质:
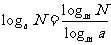 (
(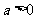 ,
,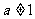 ,
,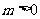 ,
, 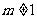 ,
,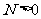 )
) 
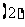
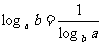 ,
,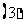
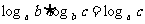 ,
, 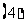
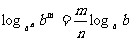
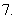 指数方程和对数方程主要有以下几种类型:
指数方程和对数方程主要有以下几种类型:
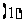
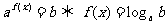 ;
;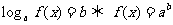 (定义法)
(定义法)
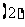
 ;
;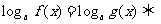
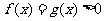 (同底法)
(同底法)
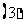
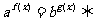
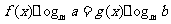 (两边取对数法)
(两边取对数法)
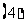

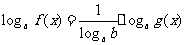 (换底法)
(换底法)
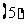
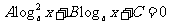 (
(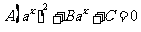 )(设
)(设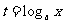 或
或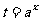 )(换元法)
)(换元法)
21.解:(1)在曲线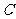 上任取一个动点P(x,y),则点(x,2y)在圆
上任取一个动点P(x,y),则点(x,2y)在圆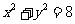 上.所以有
上.所以有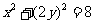 .整理得曲线C的方程为
.整理得曲线C的方程为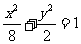 .
.
它表示一个焦点在x轴上的椭圆. …………4分
(2)∵直线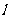 平行于OM,且在y轴上的截距为m,又
平行于OM,且在y轴上的截距为m,又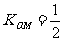 ,
,
∴直线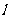 的方程为
的方程为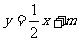 .
…………6分
.
…………6分
由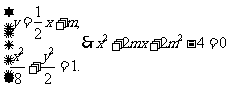 ,
…………7分
,
…………7分
∵直线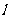 与椭圆交于A、B两个不同点,
与椭圆交于A、B两个不同点,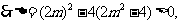 …………8分
…………8分
解得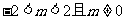 .∴m的取值范围是
.∴m的取值范围是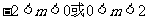 . …………10分
. …………10分
(3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.
设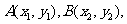
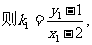
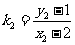 ,
, 可得
可得 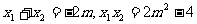 .……12分
.……12分
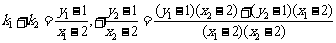
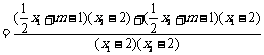
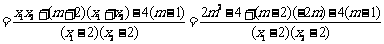
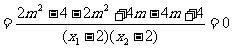 .
.
k1+k2=0.故直线MA、MB与x轴始终围成一个等腰三角形. …………14分
20.⑴ {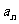 }为等差数列,∵
}为等差数列,∵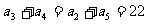 ,
,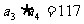 , …………1分
, …………1分
∴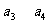 是方程
是方程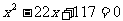 的两实根,又∵
的两实根,又∵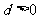 ,∴
,∴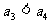 ,
,
解得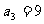 ,
,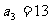 ∴
∴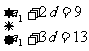 ,
…………3分
,
…………3分
解得 ,
, 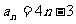 . …………4分
. …………4分
⑵ 由⑴知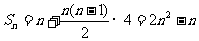 ,
…………5分
,
…………5分
∴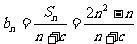 ∴
∴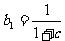 ,
,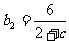 ,
,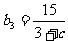 ;
…………7分
;
…………7分
∵{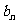 }是等差数列,∴
}是等差数列,∴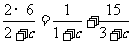 解得
解得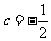 (
(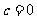 舍去). ……8分
舍去). ……8分
⑶ 由⑵得
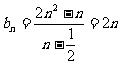 , …………9分
, …………9分
∴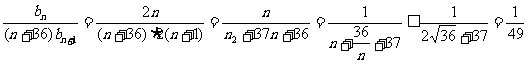 ,
,
…………12分
当且当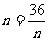 即
即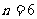 时取等号,∴
时取等号,∴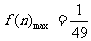 . …………14分
. …………14分
19.解:设事件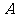 为“方程
为“方程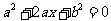 有实根”. …………1分
有实根”. …………1分
当 ,
,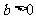 时,方程
时,方程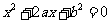 有实根的充要条件为
有实根的充要条件为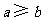 . ………3分
. ………3分
(Ⅰ)基本事件共12个:
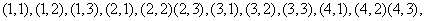 ………5分
………5分
其中第一个数表示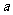 的取值,第二个数表示
的取值,第二个数表示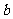 的取值.事件
的取值.事件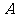 中包含9个基本事件,
中包含9个基本事件,
事件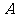 发生的概率为
发生的概率为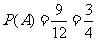 .
…………8分
.
…………8分
(Ⅱ)试验的全部结束所构成的区域为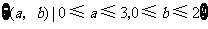 .…………10分
.…………10分
构成事件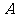 的区域为
的区域为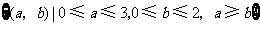 . …………12分
. …………12分
所以所求的概率为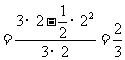 .
…………14分
.
…………14分
18.解:(1)∵PA⊥平面CDAB,AB 平面ABCD,∴PA⊥AB, …………2分
平面ABCD,∴PA⊥AB, …………2分
又AB⊥AD,PA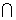 AD=A,∴AB⊥平面PAD,
…………3分
AD=A,∴AB⊥平面PAD,
…………3分
∵PD 平面PAD,∴AB⊥PD.
…………4分
平面PAD,∴AB⊥PD.
…………4分
(2)取线段PB的中点E,PC的中点F,连结AE,EF,DF,
EF是△PBC中位线,∴EF∥BC,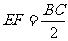 ;
…………6分
;
…………6分
又AD∥BC,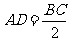 ,∴四边形EFDA是平行四边形,
…………8分
,∴四边形EFDA是平行四边形,
…………8分
∴AE∥DF,又AE 平面PDC,DF
平面PDC,DF 平面PDC,∴AE∥平面PDC,
平面PDC,∴AE∥平面PDC,
故线段PB的中点E是符合题意要求的点. …………10分
(3)设点D到平面PBC的距离为h.∵BC⊥AB,BC⊥PA,∴BC⊥平面PAB,∴BC⊥PB,
PB=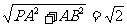 ,S△PBC=
,S△PBC=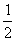 PB·BC=
PB·BC=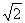 ,S△BDC=
,S△BDC=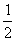 BC·AB=1 …………12分
BC·AB=1 …………12分
∵VP-BDC=VD-PBC,即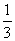 S△BDC·PA=
S△BDC·PA=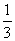 S△PBC·h ,∴h=
S△PBC·h ,∴h=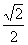 .
…………14分
.
…………14分
17.解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x=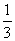 m. …………2分
m. …………2分
当x变化时,f’(x)与f(x)的变化情况如下表:
|
x |
(-∞,-m) |
-m |
(-m,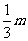 ) ) |
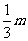 |
(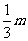 ,+∞) ,+∞) |
|
f’(x) |
 + + |
0 |
- |
0 |
+ |
|
f (x) |
|
极大值 |
|
极小值 |
|
从而可知,当x=-m时,函数f(x)取得极大值9,
即f(-m)=-m3+m3+m3+1=9, …………6分
∴ m=2. …………7分
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1, 依题意知f’(x)=3x2+4x-4=-5,
∴x=-1或x=-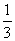 . …………9分
. …………9分
又f(-1)=6,f(-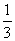 )=
)=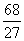 ,
…………10分
,
…………10分
所以切线方程为y-6=-5(x+1),或y-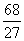 =-5(x+
=-5(x+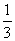 ),
),
即所求的直线方程为: 5x+y-1=0,或135x+27y-23=0 . …………12分
16.解:(1)∵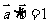 , ∴
, ∴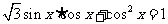 , ……………2分
, ……………2分
即 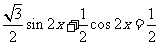 ,
……………3分
,
……………3分
∴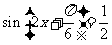 .
……………4分
.
……………4分
∵
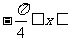
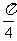 , ∴
, ∴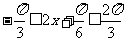 , ……………6分
, ……………6分
∴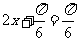 , ∴
, ∴ 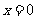 .
……………7分
.
……………7分
(2)由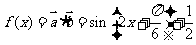 ,∴
,∴ .
…………8分
.
…………8分
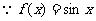 的单调减区间为
的单调减区间为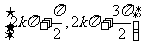 ,
,
∴ 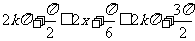 ,
…………10分
,
…………10分
∴ 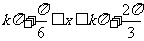 ,
,
∴ 原函数单调减区间为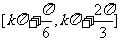
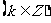 .
…………12分
.
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com