
2. D.解析:x2-1>0,x<-1或x>1,选D.
1. A.解析:当m=±2时,A={1,4},B={2,4},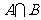 ={4},所以“m=2”是“
={4},所以“m=2”是“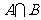 ={4}”的充分不必要条件,选A.
={4}”的充分不必要条件,选A.
21.(本小题满分14分) 设圆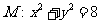 ,将曲线上每一点的纵坐标压缩到原来的
,将曲线上每一点的纵坐标压缩到原来的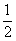 ,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线
,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线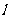 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0),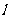 交曲线C于A、B两个不同点.
交曲线C于A、B两个不同点.
(1)求曲线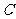 的方程;
的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.
[答案及详细解析]
20.(本小题满分14分) 已知公差大于零的等差数列{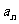 }的前n项和为
}的前n项和为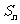 ,且满足
,且满足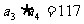 ,
,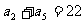 .
.
 ⑴求通项
⑴求通项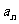 ;
;
⑵若数列
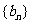 是等差数列,且
是等差数列,且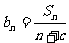 ,求非零常数c;
,求非零常数c;
⑶比较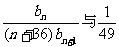 (
(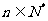 )的大小.
)的大小.
19.(本小题满分14分)
设有关于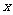 的一元二次
的一元二次
方程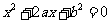 .
.
(Ⅰ)若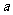 是从
是从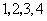 四个数中任取的一个数,
四个数中任取的一个数,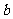 是从
是从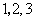 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若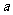 是从区间
是从区间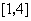 任取的一个数,
任取的一个数,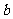 是从区间
是从区间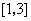 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
18.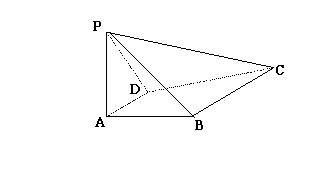 (本小题满分14分) 如图,已知四棱锥P-ABCD中,PA⊥平面CDAB, ABCD是直角梯形,AD∥BC,∠BAD
(本小题满分14分) 如图,已知四棱锥P-ABCD中,PA⊥平面CDAB, ABCD是直角梯形,AD∥BC,∠BAD 90º,BC
90º,BC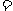 2,PA
2,PA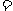 AB
AB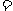 1.
1.
(1)求证:PD⊥AB;
(2)在线段PB上找一点E,使AE//平面PCD;
(3)求点D到平面PBC的距离.
17.(本小题满分12分) 已知函数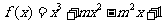 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(Ⅰ)求m的值;
(Ⅱ)若斜率为 的直线是曲线
的直线是曲线 的切线,求此直线方程.
的切线,求此直线方程.
16.(本小题满分12分) 已知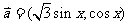 ,
,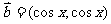 .
.
(1)若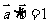 ,且
,且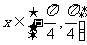 ,求
,求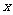 的值;
的值;
(2)设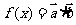 ,求
,求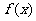 的周期及单调减区间.
的周期及单调减区间.
(二)选做题(14-15题,考生只能从中选做一题)
14. (坐标系与参数方程选做题)曲线
(坐标系与参数方程选做题)曲线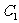 :
: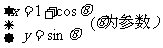 上的点到曲线
上的点到曲线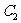 :
: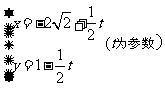 上的点的最短距离为
.
上的点的最短距离为
.
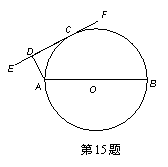
15.(几何证明选讲选做题)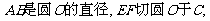
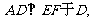
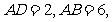 则
则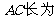 _______.
_______.
(一)必做题(11-13题)
11.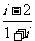 的实部为
.
的实部为
.
12.已知点P(x,y)满足条件 y的最大值为8,则
y的最大值为8,则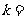 ________.
________.
13.在如图所示的算法流程图中,输出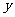 的值为
的值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com