
5.(09福建卷理)若曲线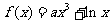 存在垂直于
存在垂直于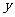 轴的切线,则实数
轴的切线,则实数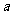 取值范围是_____________.
取值范围是_____________.
4.(09江苏卷)在平面直角坐标系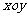 中,点P在曲线
中,点P在曲线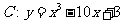 上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 .
上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 .
3.(09重庆文)把函数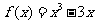 的图像
的图像 向右平移
向右平移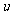 个单位长度,再向下平移
个单位长度,再向下平移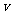 个单位长度后得到图像
个单位长度后得到图像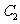 .若对任意的
.若对任意的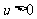 ,曲线
,曲线 与
与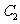 至多只有一个交点,则
至多只有一个交点,则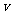 的最小值为 .
的最小值为 .
2.(09江西文)若存在过点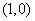 的直线与曲线
的直线与曲线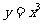 和
和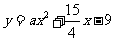 都相切,则
都相切,则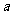 = .
= .
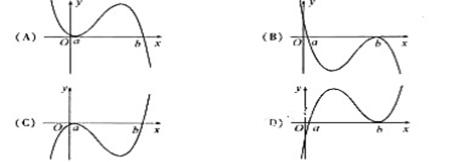
1.(09安徽理)设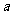 <b,函数
<b,函数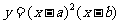 的图像可能是 (
的图像可能是 (
2.极值情况:
三次函数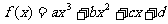 (a>0),
(a>0),
导函数为二次函数 ,
,
二次函数的判别式化简为:△=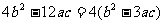 ,
,
(1) 若___________,则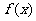 在
在 上为增函数;
上为增函数;
(2) 若____________,则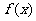 在
在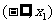 和
和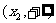 上为增函数,
上为增函数,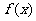 在
在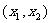 上为减函数,其中
上为减函数,其中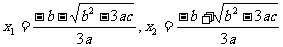 .
.
三次函数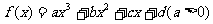 ,
,
(1) 若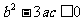 ,则
,则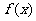 在R上无极值;
在R上无极值;
(2) 若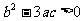 ,则
,则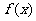 在R上有两个极值;且
在R上有两个极值;且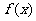 在
在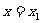 处取得极大值,在
处取得极大值,在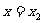 处取得极小值.
处取得极小值.
由此三次函数的极值要么一个也没有,要么有两个。
|
|
三
次 函 数 图 象 |
说
明 |
|
|
a对图象 的影响 |
 |
 |
可以根据极限的思想去分析 当a>0时,在 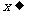 +∞右向上 伸展, +∞右向上 伸展,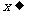 -∞左向下伸展。 -∞左向下伸展。当a<0时,在 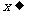 +∞右向下 +∞右向下伸展, 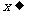 -∞左向上伸展。 -∞左向上伸展。 |
|
与x轴有三个交点 |
 |
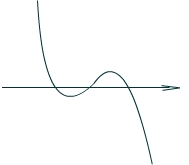 |
若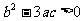 ,且 ,且 ,既两个极值异号;图象与x轴有三个交点 ,既两个极值异号;图象与x轴有三个交点 |
|
与x轴有二个交点 |
 |
 |
若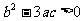 ,且 ,且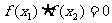 ,既有一个极值为0,图象与x轴有两个交点 ,既有一个极值为0,图象与x轴有两个交点 |
|
与x轴有一个交点 |
 |
 |
1。存在极值时即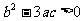 ,且 ,且 ,既两个极值同号,图象与x轴有一个交点。2。不存在极值,函数是单调函数时图象也与x轴有一个交点。 ,既两个极值同号,图象与x轴有一个交点。2。不存在极值,函数是单调函数时图象也与x轴有一个交点。 |
1.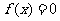 根的个数
根的个数
三次函数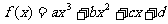
导函数为二次函数: ,
,
二次函数的判别式化简为:△=___________,
(1) 若_____________,则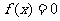 恰有一个实根;
恰有一个实根;
(2) 若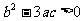 ,且_________,则
,且_________,则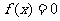 恰有一个实根;
恰有一个实根;
(3) 若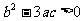 ,且__________,则
,且__________,则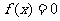 有两个不相等的实根;
有两个不相等的实根;
(4) 若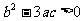 ,且____________,则
,且____________,则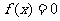 有三个不相等的实根.
有三个不相等的实根.
说明(1)(2)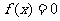 含有一个实根的充要条件是曲线
含有一个实根的充要条件是曲线 与X轴只相交一次,即
与X轴只相交一次,即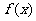 在R上为单调函数(或两极值同号),所以
在R上为单调函数(或两极值同号),所以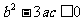 (或
(或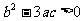 ,且
,且 ).
).
(3)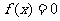 有两个相异实根的充要条件是曲线
有两个相异实根的充要条件是曲线 与X轴有两个公共点且其中之一为切点,所以
与X轴有两个公共点且其中之一为切点,所以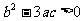 ,且
,且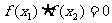 .
.
(4)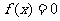 有三个不相等的实根的充要条件是曲线
有三个不相等的实根的充要条件是曲线 与X轴有三个公共点,即
与X轴有三个公共点,即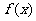 有一个极大值,一个极小值,且两极值异号.所以
有一个极大值,一个极小值,且两极值异号.所以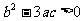 且
且 .
.
三次函数已经成为中学阶段一个重要的函数,在高考和一些重大考试中频繁出现有关它的单独命题。近年高考中,在江苏卷、浙江卷、天津卷、重庆卷、湖北卷中都出现了这个函数的单独命题,不仅仅如此,通过深化对三次函数的学习,可以解决四次函数问题。近年高考有多个省份出现了四次函数高考题,更应该引起我们的重视。单调性和对称性最能反映这个函数的特性。下面我们就来探讨一下它的单调性、对称性以及图象变化规律。
6.如图17,已知抛物线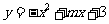 与x轴的一个交点
与x轴的一个交点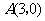 .
.
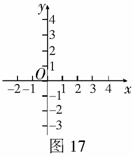
(1)你一定能分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标,试试看;
(2)设抛物线的顶点为D,请在图中画出抛物线的草图.若点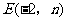 在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
(3)请设法求出tan∠DAC的值.
5.如图15,矩形ABCD中,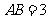 ,
,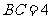 ,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,
,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积, 表示矩形NFQC的面积.
表示矩形NFQC的面积.

(1) 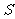 与
与 相等吗?请说明理由.
相等吗?请说明理由.
(2)设 ,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
(3)如图16,连结BE,当AE为何值时,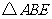 是等腰三角形.
是等腰三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com