
8. 在直角坐标系中,满足不等式 x2-y2≥0 的点(x,
y)的集合(用阴影部分来表示)的是( )
A. 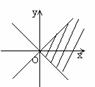 B.
B. 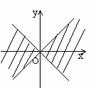 C.
C. 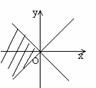 D.
D. 


7. 设函数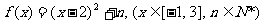 的最小值为
的最小值为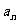 ,最大值为
,最大值为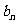 ,记
,记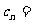
 ,则数列
,则数列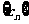 ( )
( )
A.是公差不为0的等差数列 B.是公比不为1的等比数列 
C.是常数数列
D.既不是等差数列又不是等比数列
6. 函数y= 的图像( )
的图像( )
(A) 关于原点对称
(B)关于主线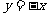 对称
对称
(C) 关于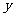 轴对称
(D)关于直线
轴对称
(D)关于直线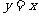 对称
对称
5. 下列函数中,最小值是4的是 (
)
A.y=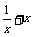 B.
B.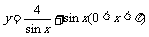

C.y=ex+4e-x D.y=log3x+4logx3(0<x<1)
3.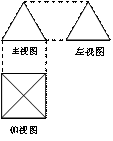 如下图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是
( )
如下图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是
( ) 
A.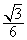 B .
B . 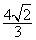

C. 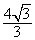 D .
D . 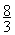




4. 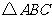 的内角
的内角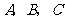 的对边分别为
的对边分别为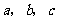 ,若
,若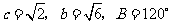 ,则
,则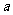 等于
(
)
等于
(
)
A. B.2 C.
B.2 C.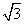 D.
D.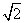

2.下列函数中,在区间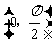 上为增函数且以
上为增函数且以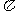 为周期的函数是(
)
为周期的函数是(
) 
A.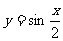 B.
B.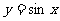 C.
C. D.
D. 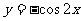

1.已知全集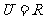 ,集合
,集合 ,
, ,则
,则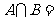 ( )
( )
A.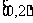 B.
B.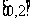 C.
C.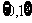 D.
D.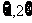

4.(09浙江理)(本题满分14分)已知函数 ,
,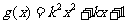 ,
,
其中 .21世纪教育网
.21世纪教育网
(I)设函数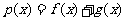 .若
.若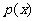 在区间
在区间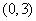 上不单调,求
上不单调,求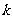 的取值范围;
的取值范围;
(II)设函数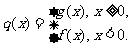 是否存在
是否存在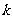 ,对任意给定的非零实数
,对任意给定的非零实数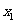 ,存在惟一
,存在惟一
的非零实数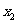 (
(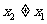 ),使得
),使得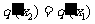 成立?若存在,求
成立?若存在,求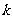 的值;若不存
的值;若不存
在,请说明理由.
由于四次函数的导函数为三次函数,所以四次函数的问题往往转化为三次函数问题
例4: 已知函数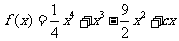 有三个极值点。
有三个极值点。
(I)证明: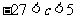 ;
;
(II)若存在实数c,使函数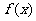 在区间
在区间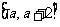 上单调递减,求
上单调递减,求 的取值范围。
的取值范围。
总结:四次函数的导数是三次函数,有三个极值点说明三次函数有三个相异的实数根。可以归结为三次函数图象与x轴有三个交点问题,可以利用第一部分很好的解决
例5:已知函数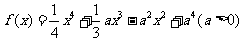
(1)求函数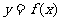 的单调区间;
的单调区间;
(2)若函数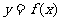 的图像与直线
的图像与直线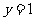 恰有两个交点,求
恰有两个交点,求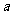 的取值范围.
的取值范围.
只要我们掌握了三次函数的这些性质,在高考中无论是主观题还是客观题,都能找到明确的解题思路,解题过程也简明扼要。四次函数问题,应该先求导,转化为三次函数问题,一般通过极值等手段解决,这些对大家来讲都是很容易的。
五当堂检测
1(09北京文)(本小题共14分)
设函数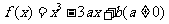 .
.
(Ⅰ)若曲线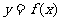 在点
在点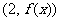 处与直线
处与直线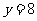 相切,求
相切,求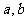 的值;
的值;
(Ⅱ)求函数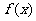 的单调区间与极值点.
的单调区间与极值点.
2(09江西文)(本小题满分12分)
设函数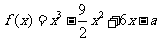 .
.
(1)对于任意实数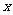 ,
,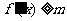 恒成立,求
恒成立,求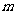 的最大值;
的最大值;
(2)若方程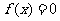 有且仅有一个实根,求
有且仅有一个实根,求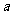 的取值范围.
的取值范围.
3.(09全国理)本小题满分12分。(注意:在试题卷上作答无效)
设函数 在两个极值点
在两个极值点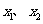 ,且
,且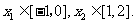
(I)求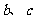 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点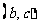 的区域;
的区域;
(II)证明: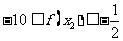
例1.讨论关于x的方程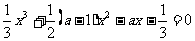 根的个数.
根的个数.
例2:设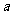 为实数,函数
为实数,函数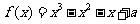 .
.
(Ⅰ)求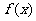 的极值;
的极值;
(Ⅱ)当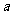 在什么范围内取值时,曲线
在什么范围内取值时,曲线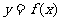 与
与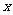 轴仅有一个交点.
轴仅有一个交点.
例3. 已知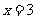 是函数
是函数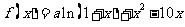 的一个极值点。
的一个极值点。
⑴求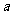 ; ⑵求函数
; ⑵求函数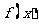 的单调区间;
的单调区间;
⑶若直线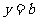 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求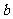 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com