
3. 已知f(x)=loga (a>0,且a≠1),则f(x)的定义域为
f(x)的奇偶性是
2.函数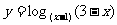 的定义域是____
____
的定义域是____
____
1.根据对数函数的图象和性质填空.
(1)已知函数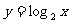 ,则当
,则当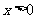 时,
时,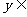 ;当
;当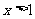 时,
时,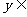 ;
;
当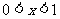 时,
时,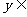 ;当
;当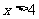 时,
时,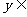 .
.
(2)已知函数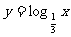 ,则当
,则当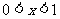 时,
时,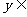 ;当
;当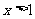 时,
时,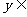 ;当
;当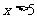 时,
时,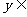 ;当
;当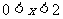 时,
时,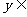 ;当
;当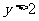 时,
时,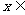 .
.
2.对数函数:
① 定义:函数 称为对数函数,
1) 函数的定义域为 __________________;
2) 函数的值域为 _____________________;
3) 当______时,函数为减函数,当______时为增函数;
4) 函数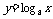 与函数
与函数 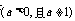 互为反函数
互为反函数
.
② 1) 图象经过点( ),图象在 ;
2) 对数函数以 为渐近线(当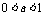 时,图象向上无限接近y轴;当
时,图象向上无限接近y轴;当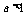 时,图象向下无限接近y轴);
时,图象向下无限接近y轴);
3) 函数y=logax与 的图象关于x轴对称.
③ 函数值的变化特征及函数图像与性质:
|
|
a>1 |
0<a<1 |
|
|
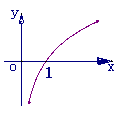
图 象 |
 |
 |
|
|
性 质 |
定义域:(0,+∞) |
||
|
值域:R |
|||
过点(1,0),即当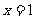 时, 时,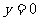 |
|||
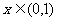 时 时 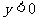  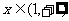 时 时 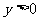  |
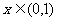 时 时 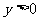  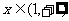 时 时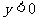  |
||
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
||
注:(1)同底的指数函数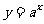 与对数函数
与对数函数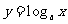 互为反函数
互为反函数
(2)底大图低
[典型例析]
例1 计算: (1)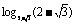
(2)2(lg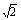 )2+lg
)2+lg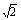 ·lg5+
·lg5+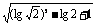 ;
;
(3)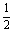 lg
lg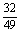 -
-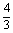 lg
lg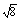 +lg
+lg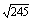 .
.
变式训练1:化简求值.
(1)log2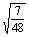 +log212-
+log212-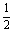 log242-1;
log242-1;
(2)(lg2)2+lg2·lg50+lg25;
(3)(log32+log92)·(log43+log83).
例2已知函数f(x)=log2(x2-ax-a)在区间(-∞,?1-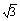 ]上是单调递减函数.求实数a的取值范围.
]上是单调递减函数.求实数a的取值范围.
例3.对于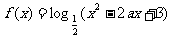 ,
,
(1)函数的“定义域为R”和“值域为R”是否是一回事;
(2)结合“实数a的取何值时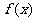 在
在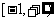 上有意义”与“实数a的取何值时函数的定义域为
上有意义”与“实数a的取何值时函数的定义域为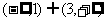 ”说明求“有意义”问题与求“定义域”问题的区别;
”说明求“有意义”问题与求“定义域”问题的区别;
(3)结合(1)(2)两问,说明实数a的取何值时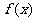 的值域为
的值域为
(4)实数a的取何值时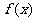 在
在 内是增函数。
内是增函数。
[当堂检测]
1.对数:
(1) 定义:如果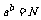
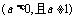 ,那么称 为
,记作
,其中
,那么称 为
,记作
,其中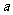 称为对数的底,N称为真数.
称为对数的底,N称为真数.
① 以10为底的对数称为常用对数,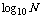 记作___________.
记作___________.
② 以无理数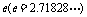 为底的对数称为自然对数,
为底的对数称为自然对数,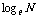 记作_________.
记作_________.
(2) 基本性质:
① 真数N为 (负数和零无对数);②  ;③
;③ 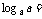 ;
;
④ 对数恒等式: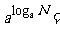 .
.
(3) 运算性质:
① loga(MN)=___________________________;
② loga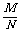 =____________________________;
=____________________________;
③ logaMn= (n∈R).
④ 换底公式:logaN= (a>0,a≠1,m>0,m≠1,N>0)
⑤ 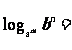 .
.
3.了解对数函数的特性以及函数的通性在解决有关问题中的灵活应用.
[学习重难点]
①理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用;
②理解对数函数的概念;理解对数函数的单调性,掌握函数图像通过的特殊点;
③知道对数函数是一类重要的函数模型;
④了解指数函数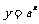 与对数函数
与对数函数 互为反函数
互为反函数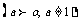
[自主学习]
2. 理解对数函数的定义、图象和性质,能利用对数函数单调性比较同底对数大小,
1. 掌握对数的预算法则
10.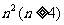 个正数排成n行n列的方阵(如右图):
个正数排成n行n列的方阵(如右图):
其中每一行的数成等差数列,每一列的数成等比数列,
并且所有的共比相等,已知: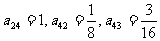
求 (1)第i行第j列交汇处的数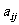 ;
;
(2)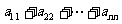 的值 .
的值 .
9.已知数列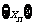 ,
,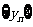 中,
中,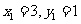 且
且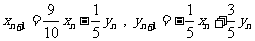 .
.
(1)是否存在实数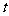 ,使
,使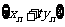 成等比数列,若存在,求出
成等比数列,若存在,求出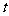 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(2)请利用(1)的结果,求出数列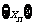 ,
,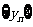 的通项公式.
的通项公式.
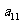
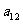
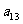
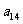

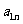
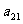
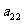
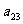
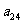

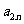
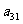
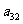
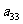
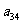


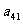
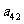
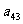
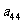

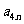






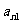
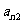
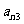
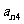

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com