
8.已知a ,b ,a+b成等差数列,a ,b, ab成等比数列,且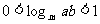 ,则m的取值范围是( )
,则m的取值范围是( )
A.(0 1) B.( 1  ) C.(0 8) D.(8
) C.(0 8) D.(8  )
)
7.设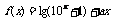 是偶函数,
是偶函数,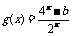 是奇函数,那么
是奇函数,那么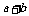 的值为 ( )
的值为 ( )
A.1 B.-1
C.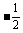 D.
D.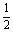
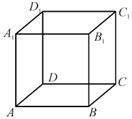
6.正方体ABCD-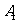
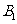
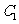
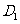 的棱上到异面直线AB, CC1的距离
的棱上到异面直线AB, CC1的距离
相等的点的个数为 ( )
A.2 B.3
C.4 D.5
5.如果函数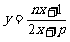 的图象关于点
的图象关于点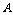 (1,2)对称,那么 ( )
(1,2)对称,那么 ( )
 A.
A.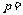 -2,
-2,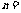 4 B.
4 B.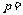 2,
2,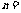 -4
-4
C.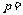 -2,
-2,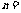 -4 D.
-4 D.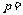 2,
2,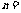 4
4
4.已知函数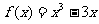 ,则
,则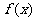 在
在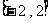 上的最大值为 ( )
上的最大值为 ( )
A.1 B.2 C.3 D.4
3.在等比数列 中,
中,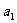 =2,前n项和
=2,前n项和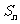 ,若
,若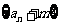
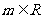 ,也是等比数列,则S
,也是等比数列,则S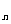 等于 ( )
等于 ( )
A.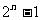 B.
B.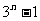 C.2n D.3n
C.2n D.3n
2.已知函数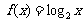 ,
,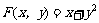 ,则
,则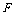 (
(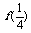 ,1)等于 ( )
,1)等于 ( )
A.-1 B.5 C.-8 D.3
1.已知集合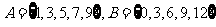 ,则
,则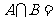 ( )
( )
A.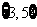 B.
B.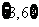 C.
C.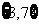 D.
D.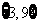
如何抓住诗歌的特点鉴赏诗歌?
研究方法:
(1)通过查找资料,了解诗歌的表现手法。如:赋、比、兴,含蓄,虚写和实写,正面描写和侧面描写,直接抒情和间接抒情,用典,象征,衬托,修辞,情景交融,托物言志和托物寓意等等。
(2)通过师生互动,掌握古诗鉴赏的基本特点、基本规律、基本方法。
基本特点:时代性,主体性,不定性。
基本规律:读懂,读通,理解,超越。
基本方法:披文人情,以义逆志,追源溯流,知人论世,想像联想,等等。
(3)通过多种形式对诗歌的相关内容进行探究。
如:开诗歌朗诵会,将诗歌改写成散文或电影小剧本,填诗填词,进行诗歌创作,等等。
(4)通过典型分析和实践,形成诗歌鉴赏的一般思路。
如:读一思一悟;明白字面意义一找出主体意象一探求深层意蕴;人一物一事一景一情;局部品味语言一捕捉隐含信息一整体把握意境一分辨表现手法一借助注释理解;了解特点流派一掌握读诗方法一整体把握诗意一实现部分突破等等。
5.古诗,为何让人百读不厌?
探究学习:古诗,经历过时间的淘洗,其存在的价值也经受住了时间的考验。古诗,是“在诗人高度敏感的情感酒窖里酿制的,有足够的力量抵御心灵的麻木”。读古诗,能“使诗歌本身的魅力一次次地深化和升华”(祝勇语)。读诗,是需要一个时间距离的。有了时间距离,古诗所焕发出的生命力,才使我们的心灵获得无限的震撼。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com