
5.)点P(3,-1)关于y轴的对称点Q的坐标是
A.(-3,-1) B.(3,1) C.(-3,1) D.(-1,3)
4.)点(3,-1)到直线3x-y=0的距离是
A. 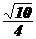 B.
B.
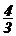 C.
C.
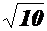 D.
D.
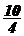
3.)直线4x-3y+12=0与圆(x-2)2+(y-2)2=9的位置关系是
A.直线过圆心 B. 相交但直线不过圆心
C.相切 D.相离
2.)“不重合的直线l1,l2的斜率相等”是“直线l1平行于直线l2”的
A.充分而非必要条件 B. 不要而非充分条件
C.充分必要条件 D.既不充分又不必要条件
1.)直线x+ky=0与2x+y-10=0垂直,则k的值为
A.2 B.-2 C.
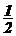 D.
D. 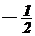
1. 选择题(每小题3分,共45分)
1直线的倾斜角
(1)当直线与X轴平行或重合是,规定次直线的倾斜角为________
(2)当直线与X轴相交是,规定把X轴绕交点按逆时针旋转到和直线重合时所转过的最小正角,叫做直线的倾斜角.所以倾斜角α的取值范围是___________________
2直线的斜率
(1) 若倾斜角α≠90 ,则直线的斜率________
,则直线的斜率________
(2) 若已知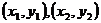 ,则直线的斜率k=
,则直线的斜率k=
3直线的方程
一般的确定一条直线主要有两个基本方面
(1) 由一个定点并依一定的方向(方向向量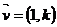 );
);
(2) 两个定点、直线的方向由倾斜角确定。即由直线的斜率确定。
|
直线名称 |
方程的形式 |
常数的意义 |
适用范围 |
|
点斜式 |
|
(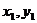 )是直线上的 )是直线上的一定点,k是斜率 |
不垂直于X轴的直线 |
|
斜截式 |
|
k是斜率,b是y轴上的截距 |
不垂直于X轴的直线 |
|
两点式 |
|
(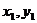 ),( ),(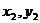 )是直线上的两定点 )是直线上的两定点 |
任何位置的直线 |
|
截距式 |
|
a,b分别是x轴、y轴上的截距 |
不垂直于坐标轴及不过原点的直线 |
|
一般式 |
|
A、B不同时为零 |
任何位置的直线 |
4要认清直线平行、垂直的充要条件,应特别注意的X,Y系数中一个为零的情况的讨论。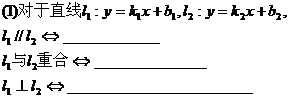
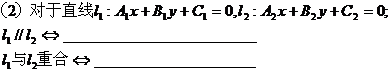
5两条直线的夹角
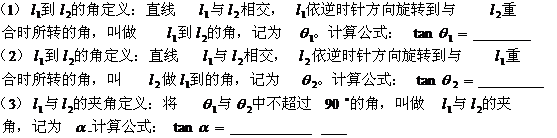
6两条直线的位置关系与方程组解的关系
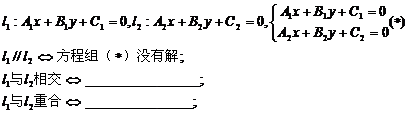
7点到直线的距离
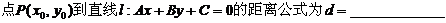
8平行直线之间的距离
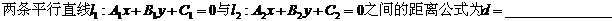
9对称问题
(1) 点点对称
A(a,b)关于P(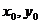 )的对称点A’(__,__)。特别地,A(a,b)关于原点O(0,0)的对称点A’’(__,__)。
)的对称点A’(__,__)。特别地,A(a,b)关于原点O(0,0)的对称点A’’(__,__)。
(2) 点关于线对称
① 点A关于轴的对称点A’(__,__)
② 点A关于轴的对称点B’(__,__)
③ 点A关于=的对称点C’(__,__)
④ 点A关于=的对称点D’(__,__)
⑤ 点A关于=的对称点E’(__,__)
⑥ 点A关于=的对称点F’(__,__)
⑦ 点A关于直线Ax+By+C=0的对称点为P(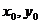 ),则P是方程组
),则P是方程组 的解,即P(__,__).
的解,即P(__,__).
(4) 线线对称
设l:Ax+By+C=0则
① l关于点A(a,b)的对称直线的方程是______________________
② l关于x轴的对称直线方程是___________________
③ l关于y轴的对称直线方程是____________________
④ l关于y=x的对称直线方程是___________________
⑤ l关于y=x+b的对称直线方程是______________________
⑥ l关于y=-x的对称直线方程是___________________
⑦ l关于y=-x+b的对称直线方程是______________________
10线性规划
(1) 二元一次不等式表示平面的区域
直线Ax+By+C=0将平面划分为三部分,即点在直线上,点在直线的上方区域,点在直线的下方区域。
l 若满足___________________,则点P(x,y)在直线的上方;
l 若满足___________________,则点P(x,y)在直线的下方。
二元一次平面区域的判定方法是:____________________-
(2) 线性规划
求线性目标函数在_________ 的最大值或最小值问题,称为线性规划问题,满足_________的解叫做可行解,由_______解组成的集合叫做__________,使目标函数取得_________ 的可行解叫做最优解。
(3) 用图解法解线性规划问题的步骤:
① 分析并将已知数据列出表格;
② 确定线性约束条件;
③ 确定线性目标函数;
④ 画出可行域;
⑤ 利用线性目标函数(直线)求出最优解;
⑥ 据实际问题的需要,适当调整最优解(如整数解等)。
11曲线和方程
(1) 在直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹)上的点与一个二元一次方程 的实数解建立了如下的关系:
①___________;②______________,那么这个方程叫做曲线的方程;这条曲线叫做方程的曲线(图形)。
点A(a,b)在曲线C:f(x,y)=0上的充要条件是:_______________
(2)借助 研究几何图形的方法叫做坐标法,用 研究几何图形的学科叫做解析几何。平面解析几何研究的主要问题是①______________________;②______________________。
12圆的方程
(1) 圆的标准方程:________________;其中圆心坐标________,半径是___。如果圆心在原点,则圆的方程为______________________。
(2) 圆的一般方程:_________________,其中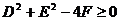 ,圆心O’(_______),半径R=____。
,圆心O’(_______),半径R=____。
特点:二次项的系数_______,2)缺_______。
二元二次方程表示圆的充要条件是
(3)圆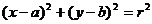 的参数方程为
的参数方程为 。特殊地,圆心在原点的圆的参数方程为
。特殊地,圆心在原点的圆的参数方程为 。
。
(4)端点圆的方程:一个圆的直径的端点是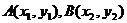 ,则圆的方程为__________________。
,则圆的方程为__________________。
(5)点与圆的位置关系:设点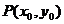 ,圆
,圆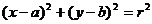 ,若P到圆心距离为d,则
,若P到圆心距离为d,则
1)d﹥r即_____________
2)d=r即_______________
3)d﹤r即点_____________
圆外一点P与圆上一点M之间距离的最大值为 ,最小值为 。
13直线和圆的位置关系
(1)直线与圆的位置关系
(2) 圆的切线
若切点P(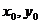 )在圆
)在圆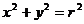 上,则切线方程为____________;若切点P(
上,则切线方程为____________;若切点P(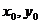 ),圆的方程为
),圆的方程为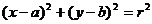 ,切线方程为________________;若切点P(
,切线方程为________________;若切点P(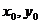 ),圆的方程为
),圆的方程为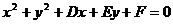 ,则切线方程为____________________。
,则切线方程为____________________。
(3) 圆的弦
过圆内一点的最长弦________;最短弦_______,当直线与圆相交时,设弦长l,弦心距d,半径为r,则有________.
当直线l斜率为k,与圆相交时,弦长
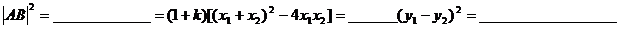
 .
.
(4) 圆与圆的位置关系
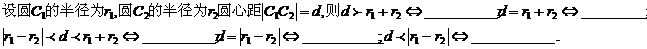
(5) 圆系方程
过直线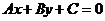 与圆
与圆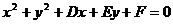 交点的圆系方程为:___________,其中λ∈R;
交点的圆系方程为:___________,其中λ∈R;
过两圆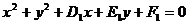 与
与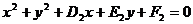 的交点的圆系方程为____________。当λ=-1且两圆相交时,会消去二次项,此时为两圆公共弦的方程。
的交点的圆系方程为____________。当λ=-1且两圆相交时,会消去二次项,此时为两圆公共弦的方程。
 (二、)圆锥曲线知识点填空
(二、)圆锥曲线知识点填空
1椭圆
(1) 平面内与两个__________________________________的点的轨迹叫椭圆,这两个定点叫椭圆的_____,两焦点的距离叫椭圆的______。
平面内动点P到一定点F和一定直线l距离之比是常数e,若_______,则动点的轨迹是椭圆,定直线l叫相应于定点F(即____)的_____。定点不在直线l上,e即是椭圆的________,这是椭圆的第二定义
|
标准方程 |
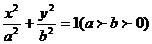 |
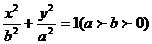 |
|
|
图形 |
|
|
|
|
性质 |
焦点 |
|
|
|
焦距 |
|
||
|
范围 |
|
|
|
|
对称中心 |
|
||
|
顶点 |
|
|
|
|
对称轴 |
|
||
|
离心率 |
|
||
|
准线方程 |
|
|
|
|
焦半径 |
|
|
|
|
特征三角 |
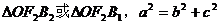 |
(2) 椭圆的标准方程和几何性质(填下表)
(3)椭圆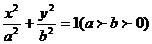 的参数方程为
的参数方程为 ( )
( )
(4)椭圆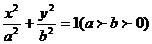 ,它的焦点与椭圆上点的最短距离______ ,最长距离_____,焦点到相应准线的距离为_____ 。当焦点弦垂直与椭圆的长轴时称为______ ,其长为
,它的焦点与椭圆上点的最短距离______ ,最长距离_____,焦点到相应准线的距离为_____ 。当焦点弦垂直与椭圆的长轴时称为______ ,其长为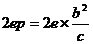 =_______。(p为焦准距)
=_______。(p为焦准距)
(5)点P(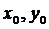 )在椭圆
)在椭圆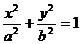 内
内 ______________________;点P(
______________________;点P(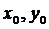 )在椭圆
)在椭圆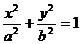 上
上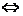 ______________________;点P(
______________________;点P(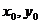 )在椭圆
)在椭圆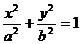 外
外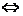 ____________________。
____________________。
(6)椭圆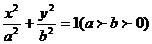 上一点P(
上一点P(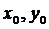 )与两焦点构成的
)与两焦点构成的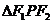 称为焦点三角形,若
称为焦点三角形,若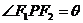 则
则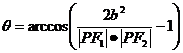 ,当
,当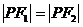 时,即P为短轴端
时,即P为短轴端
点时,θ最大,且
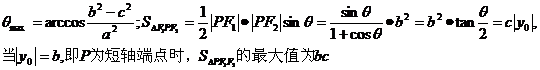
2双曲线
(1) 我们把平面内与______________ 的点的轨迹叫做双曲线.两定点叫双曲线的____,两焦点的距离叫双曲线的_____.
当动点到一定点的距离和它到一条定直线的距离的比是常数e (e_____) 时,这个点的轨迹是双曲线,定点的双曲线的 ______,定直线叫双曲线的 _____.(第二定义)
若点P在双曲线的右支上,则________ ,若点P在双曲线的左支上,则_______ .
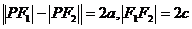 ,若______ ,则P点轨迹是双曲线;若_____ ,则P点轨迹是以为端点,_____ ;若a>c,则P点 _____.
,若______ ,则P点轨迹是双曲线;若_____ ,则P点轨迹是以为端点,_____ ;若a>c,则P点 _____.
(2)双曲线的标准方程和几何性质(填下表)
|
标准方程 |
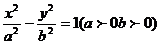 |
 |
|
|
图形 |
|
|
|
|
性质 |
焦点 |
|
|
|
焦距 |
|
||
|
范围 |
|
|
|
|
对称中心 |
|
||
|
顶点 |
|
|
|
|
对称轴 |
|
||
|
离心率 |
|
||
|
准线方程 |
|
|
|
|
渐近线 |
|
|
|
|
焦半径 |
若点P在右半支上,则 若点P在作半支上,则 |
若点P在上半支上,则 若点P在下半支上,则 |
对于等轴双曲线(a=b的双曲线),其渐近线方程为________,离心率为_______ .
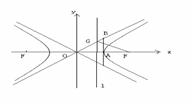
双曲线的特征三角形,如右图中△OAB,包含了双曲线的所有基本特征量:
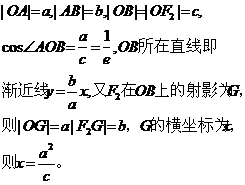
3抛物线
(1) 平面内与 ______________的点的诡计叫做抛物线.点F叫抛物线的_______
,直线叫抛物线的 _____,其中F l.
l.
(2) 抛物线的标准方程和几何性质(填下表)
|
标准方程 |
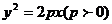 |
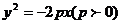 |
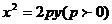 |
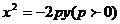 |
|
|
图形 |
|
|
|
|
|
|
性质 |
范围 |
|
|
|
|
|
准线方程 |
|
|
|
|
|
|
焦点 |
|
|
|
|
|
|
轴 |
|
|
|||
|
顶点 |
|
|
|||
|
离心率 |
|
||||
|
焦半径 |
|
|
|
|
(3) 抛物线的过焦点且垂直与对称轴的弦叫抛物线的_________ ,抛物线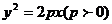 的通径长为_______ .
的通径长为_______ .
抛物线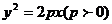 的焦点为F,过F的焦点弦AB的倾斜角为θ,则
的焦点为F,过F的焦点弦AB的倾斜角为θ,则 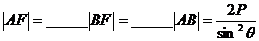 .其它形式的抛物线也有类似的结论.
.其它形式的抛物线也有类似的结论.
以上述焦点弦AB为直径的圆与其准线_________ .
4直线与圆锥曲线
设直线l:Ax+By+C=0,圆锥曲线f(x,y)=0:由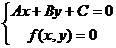 消元(x或y),若消去y得
消元(x或y),若消去y得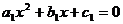 .
.
(1)
若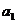 =0,此时圆锥曲线不是 ,当圆锥曲线为双曲线时,直线与双曲线的渐近线 ;当圆锥曲线是抛物线时,直线与抛物线的对称轴 .
=0,此时圆锥曲线不是 ,当圆锥曲线为双曲线时,直线与双曲线的渐近线 ;当圆锥曲线是抛物线时,直线与抛物线的对称轴 .
(2)
若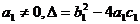 ,则
,则
1) Δ>0时,直线与圆锥曲线 ________,有 _______ 交点;
2) Δ=0时,直线与圆锥曲线 ________,有 ______的公共点;
3) Δ<0时,直线与圆锥曲线 ________,没有_____ .
(3)
设直线Ax+By+C=0与圆锥曲线f(x,y)=0相交于 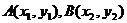 ,则弦长|AB|=_____
,则弦长|AB|=_____
若直线过圆锥曲线的焦点,当焦点弦垂直与对称轴时称为___
,其中|AB|=2ep(p为焦准距).若椭圆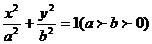 的弦AB过焦点F(-c,o),则|AB|=_____ ;若双曲线
的弦AB过焦点F(-c,o),则|AB|=_____ ;若双曲线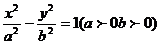 的弦AB过焦点F(-c,0),且A,B在左支,则|AB|=
________;若抛物线
的弦AB过焦点F(-c,0),且A,B在左支,则|AB|=
________;若抛物线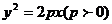 的弦AB过焦点F
的弦AB过焦点F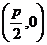 ,则|AB|=_________ .
,则|AB|=_________ .
5轨迹问题
(1) 常见的轨迹
1) 在平面内,到两定点的距离相等的点的轨迹是_____________ .
2) 平面内到角两边距离相等的点的轨迹是 _______________;
3) 平面内到定点的距离等于定长的点的诡计是 _____________-.
4) 平面内到定点的距离与到定直线的距离之比等于常数的点的轨迹是_______ .当常数大于1时,表示双曲线;当常数等于1时,表示 _________;当常数大于0而小于1时,表示________ .定点和定直线分别是圆锥曲线的 ____和 ___.
5) 平面内到定直线的距离等于某一定植的点的轨迹是 ____________.
(2) 求动点的轨迹方程的一般步骤:
1) 建系-----______________________________________;
2) 设点------_____________________________________;
3) 列式-----______________________________________;
4) 代换-----______________________________________;
5) 证明-----______________________________________;
45、(每空2分,共16分)细胞通讯是细胞间或细胞内通过高度精确和高效地发送与接收信息的通讯机制,对环境作出综合反应的细胞行为。下图A、B所示细胞通讯方式为人体内常见的两种不同类型的信号分子及其信号传导方式, C、D表示不同的信号分子对靶细胞作用的方式。
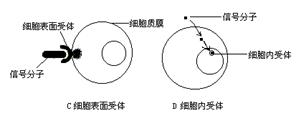
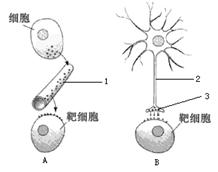
请据图回答问题:
(1)在人体内图A所示过程中的信号分子最可能的名称为 _▲ 。那么参与这类物质合成与分泌的细胞器肯定有 _▲ 种。(不得少于两种)
(2)如果图A过程表示的是胰岛素分子对机体的作用过程,那么胰岛素分子主要通过[1]
_▲ 运输途径到达所作用的靶细胞,主要的靶细胞有 _▲ 。(不得少于两种)
(3)根据C、D可知靶细胞上接受信号分子的受体有两种,一类是细胞表面受体,一类是细胞内受体。信号分子与受体结合的部位是细胞膜的特性以及信号分子的化学性质有关。下列所列物质属于信号分子并且通过细胞内的某些物质选择性的识别和结合而实现的是_▲
A.唾液淀粉酶 B.性激素 C.生长激素 D.呼吸氧化酶
(4)如果图B所示的靶细胞为人体唾液腺细胞,那么从神经调节方式的组成结构来看,[2]应该属于 _▲ 。接受[3]所释放物质的主要是该靶细胞膜上的_▲ 物质。
(5)细胞完成信号应答之后,要进行信号解除,终止细胞应答。已知[3]所释放的某种物质可使该靶细胞发生兴奋分泌唾液,当完成一次兴奋传递后,该种物质立即被分解。某种药物可以阻止该种物质的分解,这种药物的即时效应是( )
A.[2]持续性兴奋 B.靶细胞持续性兴奋并分泌唾液
C.[2]持续性抑制 D.靶细胞持续性抑制不再分泌唾液
44、(16分)下图表示下丘脑神经细胞、垂体细胞、甲状腺细胞及它们分泌的激素之间的关系,研究表明物质乙是一种糖蛋白。请回答下列问题。
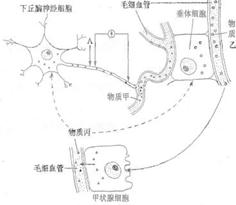 (1)图中的下丘脑神经细胞除具有神经细
(1)图中的下丘脑神经细胞除具有神经细
胞的功能外,还具有 _▲ 功能。
(2)如果用物质丙饲喂正常动物,则物质
甲、乙的分泌量的变化分别是 ▲ 、
_▲ ;如果用物质乙饲 喂正常动
物,则物质丙的分泌量__▲ ,原因
是 _▲ 。
(3)物质乙与甲状腺细胞的细胞膜表面的
▲ 结合,反映出细胞膜能进行_▲ 。
(4)若刺激图中A点,电表指针偏转的情
况是 _▲__。
43、(共9分)下图表示三个神经元及其联系。其中:“-O-<”表示从树突到细胞体,再到轴突及末梢(即一个完整的神经元模式)。为了研究兴奋在一个神经元上的传导方向和在神经元间的传递方向,进行了相关实验。根据图回答问题:
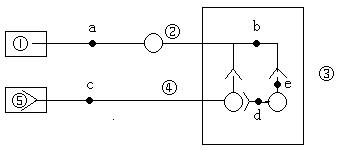
(1)若①代表感受器,⑤代表可以收缩和舒张的肌肉,则③称为 _▲ 。
(2)若刺激d点,图中有哪些点可以发生兴奋 _▲ (用字母表示)
(3)由图中可看出一个神经元的突触小体与下一个神经元的 _▲ 相接触而形成突触,图中共有突触3个。突触又由 _▲ 、_▲ 和 _▲ 三部分组成。
(4)兴奋在一个神经元上的传导方向是_▲ 。兴奋在两个神经元间的传递是 ________▲ ,其原因是 _▲ 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com