
4.在西周封国鲁国的宗法体系中,处于大宗地位的是( )
A.周王
B.鲁国国君
C.卿大夫
D.士
3.按照西周宗法制的规定,有资格继承王位的是( )
A.大哥,时年30岁,为周王妾一(俺室)所生 B.二哥,时年28岁,为周王正妻所生
C.三哥,时年25岁,为周王妾二(侧室)所生 D.四哥,时年23岁,为周王正妻所生
2.在西周分封制下,受封的诸侯在其领地内享有的权利不包括( )
A.设置官员 B.自称天子 C.建立武装 D.征派赋役
1.西周宗法制度的核心是( )
 A.大宗、小宗制 B.礼乐制度
C.世卿世禄制 D.嫡长子继承制
A.大宗、小宗制 B.礼乐制度
C.世卿世禄制 D.嫡长子继承制
学生小新读完上文,很感兴趣,他模仿着[练4]的题型,只是变了几个系数,结果成了下面的问题.
[例7] 研究函数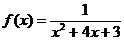 有无最值.
有无最值.
[小新解答] 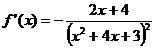 .
.
令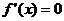 ,得
,得 的唯一驻点
的唯一驻点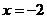 为“最点”.
为“最点”.
因此 有最值
有最值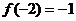 .
.
[讨论] 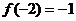 是最值吗?若为最大值,我们可以找到比它更大的
是最值吗?若为最大值,我们可以找到比它更大的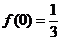 ;如果是最小值,我们可以找到比它更小的
;如果是最小值,我们可以找到比它更小的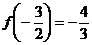 .
.
解答错了!错在哪里?作为思考题留给读者.
[提示] 本函数 的定义域不是“一个”开区间.
的定义域不是“一个”开区间.
导数应用于高考,一般都在研究函数的单调性和函数最值问题,对可导函数来讲,这两个问题互相捆绑着,于是导数问题的“根本”则变成“最根”问题.
[例6] 已知可导函数 在R上恒有
在R上恒有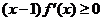 ,且
,且 不为常数,试研究
不为常数,试研究 的单调区间和函数最值.
的单调区间和函数最值.
[解析] 由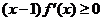 可知
可知
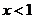 时,
时,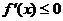 ,函数
,函数 为减函数;
为减函数;
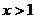 时,
时,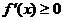 ,函数
,函数 为增函数;
为增函数;
由此可知,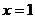 是
是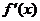 的唯一的根,故为最根.故
的唯一的根,故为最根.故 有减区间
有减区间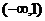 ,增区间
,增区间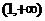 ,有最大值
,有最大值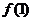 .
.
[说明] 本题是在研究“抽象函数”--无具体解析式的一类函数 的性质,只在满足性质
的性质,只在满足性质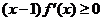 条件下,通过“最根”的判定而确定了
条件下,通过“最根”的判定而确定了 的单调区间和最值.
的单调区间和最值.
有些不等式的证明,还可以通过构造函数,研究这个函数的“最值”而确认不等式是否成立.
[练6] 已知函数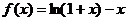 ,
,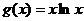 .
.
(1)求函数 的最大值;
的最大值;
(2)设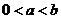 ,证明:
,证明: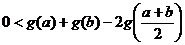 .
.
[解析] (1)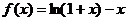
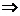
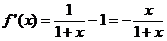 ,
,
故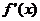 有唯一的最根
有唯一的最根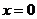 ,
,
故 的最大值为
的最大值为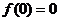 .
.
(2)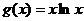 ,
,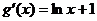 .
.
设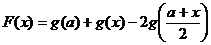 ,
,
则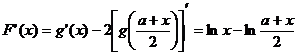 .
.
当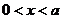 时,
时,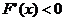 ,因此
,因此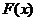 在
在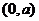 内为减函数.
内为减函数.
当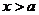 时,
时,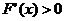 ,因此
,因此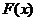 在
在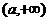 上为增函数.
上为增函数.
从而,当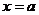 时,
时,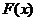 有最小值
有最小值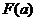 ,
,
因为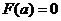 ,
,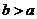 ,所以
,所以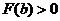 ,即
,即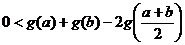 .
.
[说明] 问题(2)的解决,是用“最根”证明不等式.
若定义在一个开区间上的函数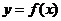 有导函数
有导函数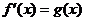 存在,那么
存在,那么 是否有最值的问题可转化为
是否有最值的问题可转化为 的导函数
的导函数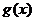 是否有最根的问题来研究:
是否有最根的问题来研究:
(1)若导函数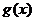 无根,即
无根,即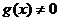 ,则
,则 无最值;
无最值;
(2)若导函数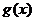 有唯一的根
有唯一的根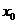 ,即
,即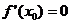 ,则
,则 有最值
有最值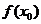 .此时,导函数
.此时,导函数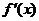 的根
的根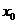 即是函数
即是函数 最根
最根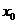 .
.
(3)若导函数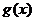 有多个的根,则应从多个驻点中依次判定极点、最点的存在性.
有多个的根,则应从多个驻点中依次判定极点、最点的存在性.
[例5] 在以下四个函数中,有最值存在的函数是
A.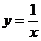 B.
B.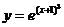 C.
C.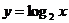 D.
D.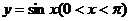
[解析] 对于A,定义区间虽有两个,但都有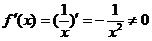 ,
, 无最值;
无最值;
对于B,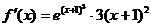 ,函数有重合的两驻点
,函数有重合的两驻点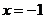 ,
, 无最值;
无最值;
对于C,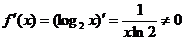 ,
, 无最值;
无最值;
对于D,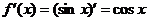 .
.
当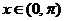 时,令
时,令 ,得
,得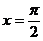 ,
, 有最值
有最值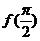 =1.
=1.
本题答案为D.
[练5] 判断以下函数,是否有最值,如果有,求出最值.
(1)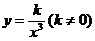 (2)
(2)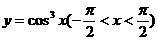
[解析] (1)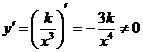 ,
, 无最值.
无最值.
(2)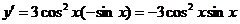 .
.
当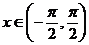 时,
时,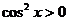 ,由
,由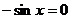 ,得
,得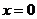 .
.
 有最值,
有最值,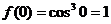 .
.
当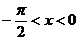 时,
时, ,
,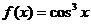 是增函数.
是增函数.
当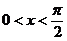 时,
时,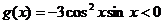 ,
,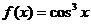 是减函数.
是减函数.
故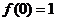 是
是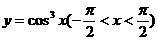 的最大值.
的最大值.
不重合的2个驻点可以分别成为极点.那么,在什么条件下极点成为最点呢?
驻点是极点的必要不充分条件,那么极点是最点的什么条件呢?
我们研究,极点何时成为最点.
[例4] 已知 的导函数
的导函数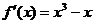 ,试探究
,试探究 的极点和最点.
的极点和最点.
[解析] 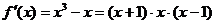 .
.
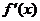 有3个相异的根:
有3个相异的根: 它们都是
它们都是 的极点.
的极点.
易知原函数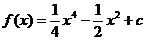 (
(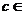 R)
R)
易知 为
为 的减区间,
的减区间,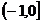 为
为 的增区间,
的增区间,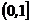 为
为 的减区间,
的减区间,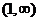 为
为 的增区间.
的增区间.
 的4个单调区间依次成“减--增--减--增”的顺序,使得首、尾两个区间的单调性相异,从而使得
的4个单调区间依次成“减--增--减--增”的顺序,使得首、尾两个区间的单调性相异,从而使得 在“两次探底”中得到最(小)点.
在“两次探底”中得到最(小)点.
比较三个极值的大小: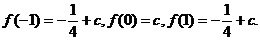
得 的最小值为
的最小值为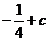 ,对应两个最小点
,对应两个最小点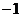 和1.
和1.
[说明] 定义在一个开区间上的可导函数 如果有n个极点:x1<x2<…<xn.
如果有n个极点:x1<x2<…<xn.
当n为奇数时, 有最点存在.最点在依次为奇数的极点中产生,通过奇数位上的极值比大小可得.
有最点存在.最点在依次为奇数的极点中产生,通过奇数位上的极值比大小可得.
当n为偶数时,函数无最点.
[练4] 求函数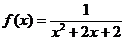 的最值.
的最值.
[解析] 函数 是定义在一个开区间
是定义在一个开区间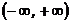 上的可导函数,
上的可导函数,
令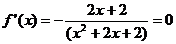
得 的唯一驻点
的唯一驻点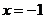 即为最点.
即为最点.
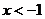 时,
时,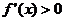 ,函数递增,
,函数递增,
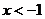 时,
时,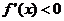 ,函数递减,
,函数递减,
故 有最大值
有最大值 .
.
[说明] 本函数是二次函数的复合函数,用配方法求最值也很简便.
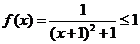 ,等号成立条件是
,等号成立条件是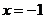 .
.
一次函数没有驻点,自然没有最点.
二次函数有一个驻点,这个驻点就是二次函数的最点.
三次函数呢?
三次函数的导函数是二次函数,这个二次函数根的情况有3种:(1)有2个相异的根,(2)有2个相同的根;(3)无根.
如果三次函数 的导函数
的导函数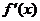 无根,则
无根,则 无驻点,自然也无最点,也无最值.
无驻点,自然也无最点,也无最值.
如果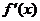 有根呢?自然
有根呢?自然 一定有驻点.
一定有驻点.
那么,这些驻点是否为其最点呢?
[例3] 研究函数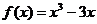 的驻点、极点和最点.
的驻点、极点和最点.
[解析] 令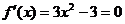 ,得
,得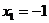 ,
,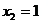 为
为 的2个驻点.
的2个驻点.
(1)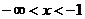 时,
时,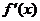 >0,函数递增;
>0,函数递增;
(2)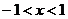 时,
时,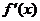 <0,函数递减;
<0,函数递减;
(3)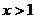 时,
时,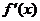 >0,函数递增.
>0,函数递增.
故 在
在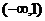 有极大值
有极大值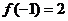 ,在
,在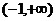 上有极小值
上有极小值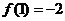 .
.
故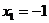 ,
,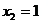 是
是 的2个极点,前者为极大点,后者为极小点.
的2个极点,前者为极大点,后者为极小点.
又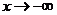 时,
时,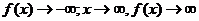 ,故函数
,故函数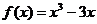 既无最大值,也无最小值.从而
既无最大值,也无最小值.从而 无最点.
无最点.
[说明] 这是三次函数有2个驻点,且都为极点的例子.而三次函数无驻点或有驻点但不是极点的例子如下(练3).
[练3] 研究下列三次函数的驻点、极点、最点和单调区间.
(1)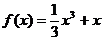 (2)
(2)
[解析] (1)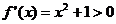 ,函数
,函数 无驻点,无极点,无最点.
无驻点,无极点,无最点.  是
是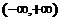 上的增函数.
上的增函数.
(2)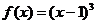 ,
,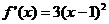
 有2个重合的驻点
有2个重合的驻点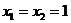 .
.
(1)当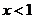 时,
时,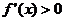 ,函数递增,
,函数递增,
(2)当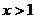 时,
时,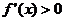 ,函数也递增.
,函数也递增.
因此,驻点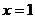 不能分出两个“相异”的单调区间,故
不能分出两个“相异”的单调区间,故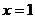 不是
不是 的极点,
的极点, 无极点,当然也无最点.
无极点,当然也无最点.
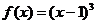 是R上的增函数.
是R上的增函数.
[说明] 函数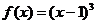 相重合的两驻点
相重合的两驻点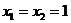 不成为极点,可理解为它们消去了“中间”的一个“相异”的单调区间后,将两边的“同性”的单调区进行了链接而成为一个单调区间.
不成为极点,可理解为它们消去了“中间”的一个“相异”的单调区间后,将两边的“同性”的单调区进行了链接而成为一个单调区间.
经过以上的讨论得知,定义在R上的三次函数,不管它有无驻点或极点,它是不会有最点的.
高中生将“最点”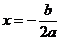 变形为
变形为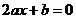 ,并由此得到一个一次函数
,并由此得到一个一次函数 .
.
精明的学生发现,这个一次函数 与对应的二次函数
与对应的二次函数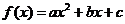 有某种“关系”,甚至有学生在偷偷地利用这种“关系”.
有某种“关系”,甚至有学生在偷偷地利用这种“关系”.
这种“关系”到了高三才彻底解决:函数 正是函数
正是函数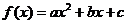 的导函数,即
的导函数,即 .
.
函数求“最根”的问题,正好是 的导函数
的导函数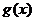 的“求根”问题.
的“求根”问题.
导函数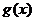 的根,就是
的根,就是 的驻点.很清楚,二次函数的驻点就是二次函数的最点.
的驻点.很清楚,二次函数的驻点就是二次函数的最点.
问题变得这么明朗:求 的最点,就是求
的最点,就是求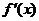 的根.俗说中“最根”,真的与“根”字巧合了.
的根.俗说中“最根”,真的与“根”字巧合了.
[例2] 设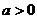 ,在同一坐标系中,分别作得
,在同一坐标系中,分别作得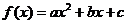 和
和 的图象(如右).
的图象(如右).
试说明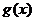 的正负性与
的正负性与 单调性的对应关系.
单调性的对应关系.
[解析] 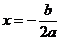 与
与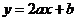 相交于
相交于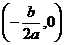 .
.
 (1)
(1)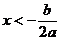 时,
时,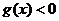 ,
, 递减;
递减;
(2)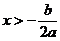 时,
时,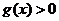 ,
, 递增;
递增;
(3)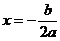 时,
时,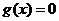 ,
, 得到最小值.
得到最小值.
故对应关系为:(1)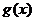 负区与
负区与 的减区对应;
的减区对应;
(2)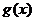 正区与
正区与 的增区对应;
的增区对应;
(3)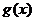 零点与
零点与 的最值对应.
的最值对应.
[练2] 已知二次函数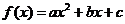 的导函数
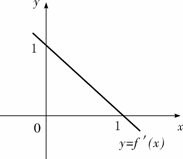
的导函数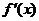 图象如右图的直线,则有
图象如右图的直线,则有
 (1)
(1)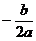 =( ),增区间为( ),减区间为( );
=( ),增区间为( ),减区间为( );
(2) 的最( )值为( );
的最( )值为( );
(3)若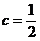 ,求
,求 的解析式.
的解析式.
[解答] 从右图上看到
(1)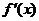 的根为
的根为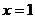 ,故有
,故有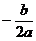 =1;
=1;
(2)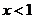 时,
时,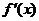 >0,故
>0,故 的增区间为
的增区间为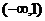 ;
;
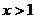 时,
时,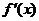 <0,故
<0,故 的减区间为
的减区间为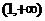 ;
;
(3) 有最大值,最大值为
有最大值,最大值为 .
.
(4)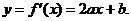

令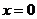 ,图上知
,图上知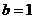 ;
;
令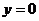 ,得
,得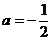 .
.
故有 .
.
[说明] 注意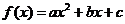 与
与 并非一一对应,每一个这样的
并非一一对应,每一个这样的 都对应着一个确定的
都对应着一个确定的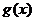 ,反过来,每一个这样的
,反过来,每一个这样的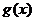 却对应着无穷个
却对应着无穷个 ,它们只是相差一个常数c.这就是本题中,为什么已经知道了
,它们只是相差一个常数c.这就是本题中,为什么已经知道了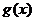 的图象后,还要给出
的图象后,还要给出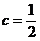 时才能确定
时才能确定 的解析式.
的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com