
8、对于函数①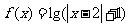 ,②
,②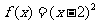 ,③
,③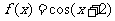 ,判断如下三个命题的真假:
,判断如下三个命题的真假:
命题甲: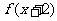 是偶函数;
是偶函数;
命题乙: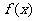 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
命题丙: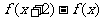 在
在 上是增函数.
上是增函数.
能使命题甲、乙、丙均为真的所有函数的序号是( )
A.①③ B.①② C.③ D.②
7、函数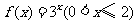 的反函数的定义域为( )
的反函数的定义域为( )
A. B.
B.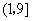 C.
C.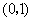 D.
D.
6、定义在R上的函数f (x)既是奇函数,又是周期函数,T是它的一个正周期.若将方程f (x)=0在闭区[-T,T]上的根的个数记为n,则n可能为
(A)0 (B)1 (C)3 (D)5
5、设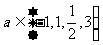 ,则使函数
,则使函数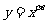 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有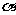 值为
值为
(A)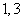 (B)
(B) 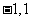 (C)
(C)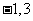 (D)
(D) 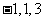
4、设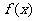 是定义在
是定义在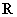 上的奇函数,且当
上的奇函数,且当 时,
时,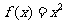 ,若对任意的
,若对任意的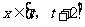 ,不等式
,不等式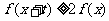 恒成立,则实数
恒成立,则实数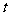 的取值范围是( )
的取值范围是( )
A.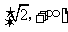 B.
B.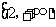 C.
C.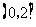 D.
D.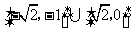
3、函数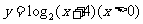 的反函数是( )
的反函数是( )
A. B.
B. C.
C.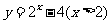 D.
D.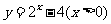
2、在R上定义的函数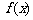 是偶函数,且
是偶函数,且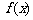
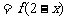 .若
.若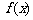 在区间
在区间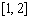 上是减函数,则
上是减函数,则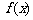 ( )
( )
A.在区间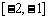 上是增函数,在区间
上是增函数,在区间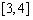 上是减函数
上是减函数
B.在区间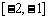 上是增函数,在区间
上是增函数,在区间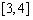 上是减函数
上是减函数
C.在区间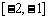 上是减函数,在区间
上是减函数,在区间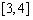 上是增函数
上是增函数
D.在区间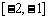 上是减函数,在区间
上是减函数,在区间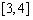 上是增函数
上是增函数
1、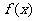 ,
,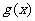 是定义在R上的函数,
是定义在R上的函数,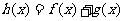 ,则“
,则“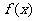 ,
,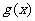 均为偶函数”是“
均为偶函数”是“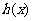 为偶函数”的
为偶函数”的
A.充要条件 B.充分而不必要的条件
C.必要而不充分的条件 D.既不充分也不必要的条件
10.若点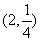 既在函数
既在函数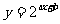 的图象上,又在它的反函数的图象上,则
的图象上,又在它的反函数的图象上,则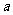 =__,
=__,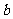 =___
=___
典型例题
EG1.已知函数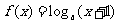 ,
,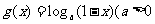 ,且
,且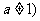
(1) 求函数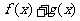 定义域
定义域
(2) 判断函数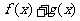 的奇偶性,并说明理由.
的奇偶性,并说明理由.
变式1:已知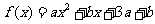 是偶函数,定义域为
是偶函数,定义域为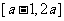 .则
.则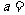 ,
,
变式2:函数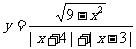 的图象关于 ( )
的图象关于 ( )
A.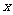 轴对称
B.
轴对称
B.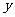 轴对称 C.原点对称 D.直线
轴对称 C.原点对称 D.直线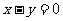 对称
对称
EG2、已知函数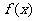 是偶函数,而且在
是偶函数,而且在 上是减函数,判断
上是减函数,判断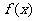 在
在 上是增函数还是减函数,并证明你的判断.
上是增函数还是减函数,并证明你的判断.
变式1:下列函数中,在其定义域内既是奇函数又是减函数的是
A.
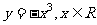 B.
B. 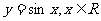 C.
C. 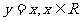 D.
D.
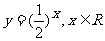
变式2:函数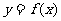 是R上的偶函数,且在
是R上的偶函数,且在 上是增函数,若
上是增函数,若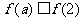 ,则实数
,则实数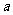 的取值范围是 ( )
的取值范围是 ( )
A.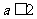 B.
B. C.
C.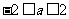 D.
D. 或
或
设计意图:考察函数奇偶性与单调性的关系
EG3、已知函数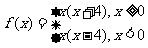 ,求
,求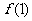 ,
,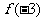 ,
, 的值
的值
变式1:设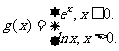 则
则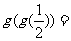 __________
__________
变式2:已知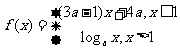 是
是 上的减函数,那么
上的减函数,那么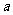 的取值范围是
的取值范围是
A.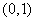 B.
B.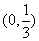 C.
C.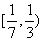 D.
D.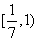
变式3:设函数f(x)=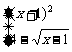
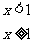 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
A.(-∞,-2]∪[0,10] B.(-∞,-2]∪[0,1]
C.(-∞,-2]∪[1,10] D.[-2,0]∪[1,10]
EG4、试着举几个满足“对定义域内任意实数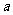 ,
,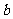 ,都有
,都有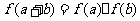 ”的函数例子.
”的函数例子.
变式1:设函数f(x)的定义域是N*,且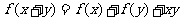 ,
,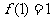 ,则f(25)= _______________.
,则f(25)= _______________.
变式2:设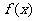 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线 对称,对任意
对称,对任意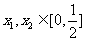 ,都有
,都有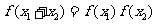
(1)设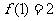 ,求
,求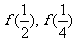
(2)证明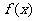 是周期函数.
是周期函数.
变式3:设函数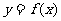 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有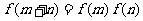 且当
且当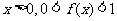
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)|f(x2)·f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,
a∈R},若A∩B= ,求a的取值范围.
,求a的取值范围.
变式4:已知函数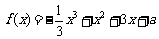 .
.
(1)求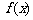 的单调减区间;
的单调减区间;
(2)若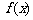 在区间
在区间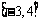 上的最小值为
上的最小值为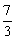 ,求
,求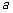 的值.
的值.
EG5、已知函数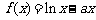
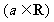 .
.
(Ⅰ) 求函数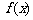 的单调区间;
的单调区间;
(Ⅱ) 当a >0时,求函数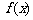 在
在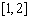 上最小值.
上最小值.
变式1:函数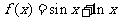 的导函数
的导函数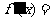 .;
.;
变式2: 函数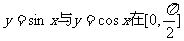 内的交点为P,它们在点P处的两条切线与x轴所围成的三角形的面积为
内的交点为P,它们在点P处的两条切线与x轴所围成的三角形的面积为
变式3:已知函数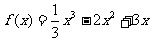 (
(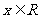 )的图象为曲线
)的图象为曲线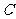 .
.
(1)求过曲线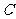 上任意一点的切线斜率的取值范围;
上任意一点的切线斜率的取值范围;
(2)若在曲线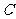 上存在两条相互垂直的切线,求其中一条切线与曲线
上存在两条相互垂直的切线,求其中一条切线与曲线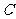 的切点的横
的切点的横
坐标的取值范围;
实战演练
9.函数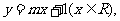 与
与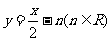 互为反函数的充要条件是___________.
互为反函数的充要条件是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com