
请把解答过程写在答题卡相应位置上.)
17. (本小题满分10分)在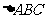 中,
中,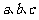 分别为角
分别为角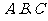 的对边,且满足
的对边,且满足 .
.
(Ⅰ)求角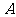 的值;
的值;
(Ⅱ)若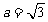 ,设角
,设角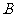 的大小为
的大小为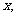
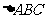 的周长为
的周长为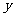 ,求
,求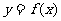 的最大值.
的最大值.
答案:(Ⅰ)在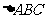 中,由
中,由 及余弦定理,得
及余弦定理,得
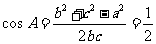 ,………………3分
,………………3分
而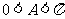 ,则
,则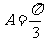 .
……………5分
.
……………5分
(Ⅱ)由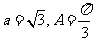 及正弦定理,得
及正弦定理,得
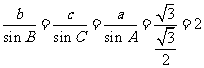 ,
,
而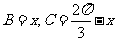 ,则
,则
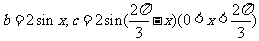 .………………7分
.………………7分
于是 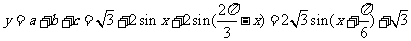 ,
,
由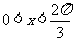 ,得
,得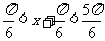 ,
,
当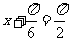 即
即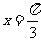 时,
时,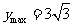 . ………………10分
. ………………10分
16. 设点P是圆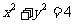 上的任一点,定点D的坐标为(8,0).当点P在圆上运动时,则线段PD的中点M的轨迹方程是__________________.
上的任一点,定点D的坐标为(8,0).当点P在圆上运动时,则线段PD的中点M的轨迹方程是__________________.
答案: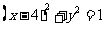 .设点M的坐标为
.设点M的坐标为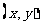 ,点P的坐标为
,点P的坐标为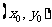 ,则
,则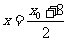 ,
,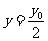 .即
.即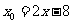 ,
,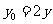 .因为点P
.因为点P 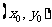 在圆
在圆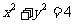 上,所以
上,所以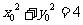 .即
.即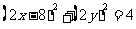 ,即
,即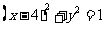 ,这就是动点M的轨迹方程.
,这就是动点M的轨迹方程.
15.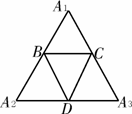 将三棱锥A-BCD沿三条侧棱剪开,
将三棱锥A-BCD沿三条侧棱剪开,
展开图形是一个边长为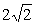 的正
的正
三角形(如图所示),则该三棱锥的
外接球的表面积是______.
答案:3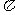 . 由题意,三棱锥A-BCD是一个棱长为
. 由题意,三棱锥A-BCD是一个棱长为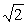 的正四面体,该三棱锥的外接球的半径是
的正四面体,该三棱锥的外接球的半径是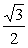 ,因此该三棱锥的外接球的表面积是
,因此该三棱锥的外接球的表面积是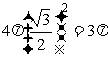 .
.
14. 在数列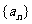 中,
中,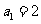 ,当n为正奇数时,
,当n为正奇数时,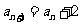 ;当n为正偶数时,
;当n为正偶数时,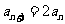 ,则
,则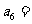 ______.
______.
答案:22. 逐渐计算,可以得到:当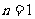 时,
时,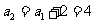 ;当
;当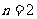 时,
时,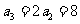 ;当
;当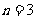 时,
时,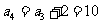 ;当
;当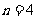 时,
时,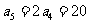 ,当
,当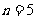 时,
时,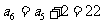 .
.
13. (理科)计算某项税率,需用公式y=(1-5x)n (n∈N* ).现已知y的展开式中各项的二项式系数之和是64,用四舍五入的方法计算当x=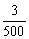 时y的值,若精确到0.001,其千分位上的数字应是
.
时y的值,若精确到0.001,其千分位上的数字应是
.
答案:3 由2n=64,得n=6. 于是 y=C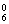 +C
+C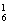 ·
·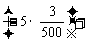 C
C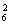
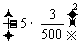
=1-0.18+0.0135=0.8335.
(文科)在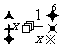 的展开式中,
的展开式中,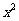 的系数为_______________.
的系数为_______________.
答案:15. 由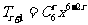 ,得
,得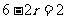 ,
,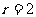 ,所以
,所以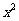 的系数为
的系数为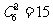 .
.
12. 设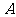 是整数集的一个非空子集,对于
是整数集的一个非空子集,对于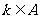 ,如果
,如果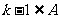 且
且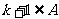 ,那么
,那么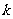 是
是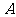 的一个“孤立元”,给定
的一个“孤立元”,给定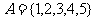 ,则
,则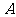 的所有子集中,只有一个“孤立元”的集合共有( )
的所有子集中,只有一个“孤立元”的集合共有( )
A.10个 B.11个 C.12个 D.13个
答案:D.“孤立元”是1的集合: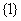 ;
;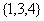 ;
;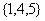 ;
;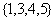 ;
;
“孤立元”是2的集合: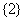 ;
;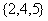 ;
;
“孤立元”是3的集合: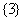 ;
;
“孤立元”是4的集合: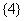 ;
;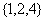 ;
;
“孤立元”是5的集合: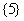 ;
;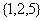 ;
;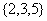 ;
;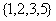 .
.
第Ⅱ卷(非选择题,共90分)
11. 如果以原点为圆心的圆经过双曲线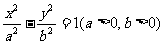 的焦点,而且比被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于( )
的焦点,而且比被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于( )
A. B.
B.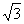 C.
C. 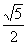 D.
D.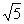
答案:A.圆的方程为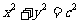 ,右准线的方程是
,右准线的方程是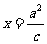 ,它与圆在第一象限的交点记为P.由题意可得,直线OP的方程为
,它与圆在第一象限的交点记为P.由题意可得,直线OP的方程为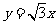 .将
.将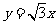 和
和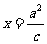 代入
代入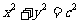 ,有
,有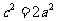 ,即
,即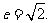
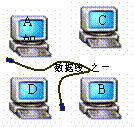
10. 如图,要用三根数据线将四台电脑A、B、C、D连接
起来以实现资源共享,则不同的连接方案的种数是(
A.16 B.18
C.20 D.22
答案:画一个正方形和它的两条对角线,在这6条线段中,选3条的选法
有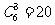 种.当中,4个直角三角形不是连接方案,故不同的连接方案共
种.当中,4个直角三角形不是连接方案,故不同的连接方案共
有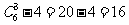 种.
种.
9. 抛物线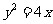 的焦点为F, 经过点F的直线与抛物线相交于A、B两点,且
的焦点为F, 经过点F的直线与抛物线相交于A、B两点,且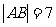 ,则线段AB 中点的横坐标是( )
,则线段AB 中点的横坐标是( )
A.2
B. 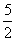 C. 3
D.
C. 3
D. 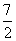
 答案:B.抛物线
答案:B.抛物线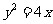 的焦点为F
的焦点为F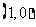 , 设经过点F的直线与抛物线相交于A、B两点,其横坐标分别为
, 设经过点F的直线与抛物线相交于A、B两点,其横坐标分别为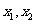 ,利用抛物线定义,AB 中点横坐标为
,利用抛物线定义,AB 中点横坐标为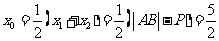 .
.
8. 如果 ,且
,且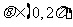 ,那么角
,那么角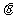 的取值范围是( )
的取值范围是( )
A.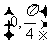 B.
B.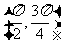 C.
C.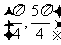 D.
D. 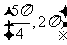
答案:C. 注意到已知不等式等价与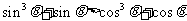 .
.
显然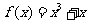 是
是 上的增函数,于是有不等式
上的增函数,于是有不等式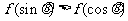 ,从而,得
,从而,得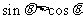 ,再结合
,再结合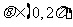 ,便得
,便得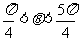 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com