
1.下列变化中没有生成新物质的是( )
A.燃放烟花 B.食物腐烂 C.剪贴窗花 D.钢铁生锈
(17)(本小题满分l2分)
设数列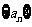 满足
满足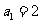 ,
,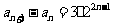
(Ⅰ)求数列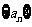 的通项公式:
的通项公式:
(Ⅱ)令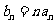 ,求数列
,求数列 的前n项和
的前n项和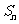 .
.
[答案]
解:
(I)由已知,当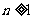 时,
时,
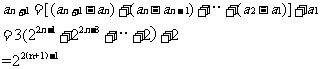
而 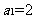
所以数列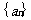 的通项公式为
的通项公式为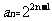
(II)由 可知
可知

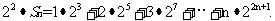
则,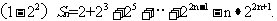
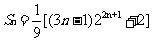
(18)(本小题满分12分)
如圈,己知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,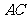 ⊥BD垂足为H,PH是四棱锥的高,E为AD中点.
⊥BD垂足为H,PH是四棱锥的高,E为AD中点.
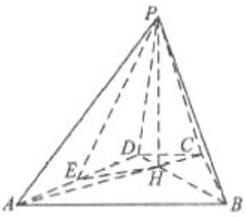 (Ⅰ)证明:PE⊥BC
(Ⅰ)证明:PE⊥BC
(Ⅱ)若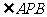 =
=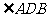 =60°,求直线PA与平面PEH所成角的正弦值.
=60°,求直线PA与平面PEH所成角的正弦值.
[答案]
解:
(I)以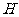 为原点,
为原点,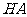 ,
,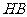 ,
,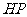 分别为
分别为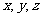 轴,线段
轴,线段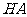 的长为单位长度,建立坐标系如图所示。
的长为单位长度,建立坐标系如图所示。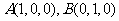
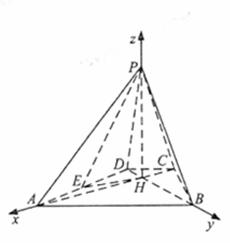
设
则 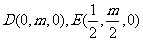
可得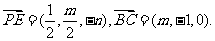
∵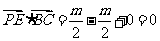
∴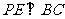
(II)由已知条件可得 ,则
,则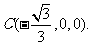
∴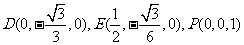
设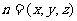 是平面
是平面 的法向量
的法向量
则
∴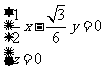
因此可以取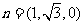
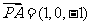
可得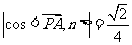
∴直线 和平面
和平面 所成角的正弦值为
所成角的正弦值为
(19)(本小题满分12分)
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:

(Ⅰ)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.

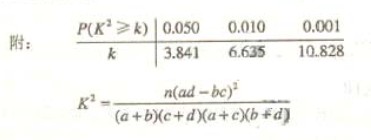
[答案]
解:
(I)调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例估计值为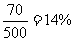
(II) 
∵9.967>6.635,∴有99%的把握认为该地区的老年人是否需要帮助与性别有关
(III)由(II)的结论可知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样的方法比采用简单随机抽样方法更好。
(20)(本小题满分12分)
设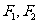 分别是椭圆E:
分别是椭圆E: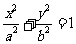 (a>b>0)的左、右焦点,过
(a>b>0)的左、右焦点,过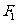 斜率为1的直线l与E 相较于A,B两点,且
斜率为1的直线l与E 相较于A,B两点,且 ,
,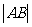 ,
,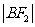 成等差数列.
成等差数列.
(Ⅰ)求E的离心率;
(Ⅱ)设点P(0,-1)满足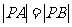 ,求E的方程.
,求E的方程.
[答案]
解:
由椭圆定义知 ,又
,又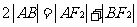
得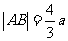
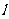 的方程为
的方程为 ,其中
,其中
设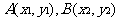 ,则
,则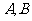 两点坐标满足方程组
两点坐标满足方程组
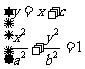
化简得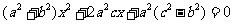
则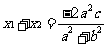 ,
,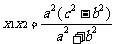
因为直线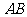 斜率为1,所以
斜率为1,所以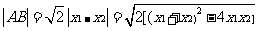
得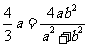
∴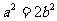
∴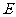 的离心率
的离心率
(II)设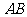 中点为
中点为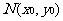 ,由(I)知
,由(I)知
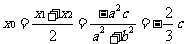 ,
,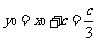
由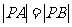 得
得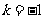
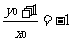
得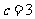
∴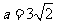 ,
,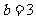
∴轨迹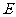 的方程为
的方程为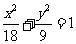
(21)(本小题满分12分)
设函数f(x)=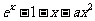 .
.
(Ⅰ)若a=0,求f(x)的单调区间;
(Ⅱ)若当x≥0时f(x)≥0,求a的取值范围.
[答案]
解:
(I) 时,
时,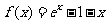 ,
,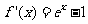
当 时,
时,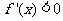 ,当
,当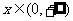 时,
时,
故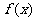 在
在 上单调递减,在
上单调递减,在 单调递增
单调递增
(II)
由(I)可知 ,当且仅当
,当且仅当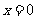 时等号成立,故
时等号成立,故
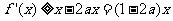
∴当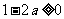 ,即
,即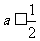 时,
时, ,
,
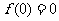
∴当 时,
时,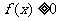
由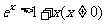 可得
可得
则当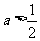 时,
时,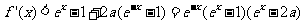
∴当 时,
时,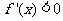 ,而
,而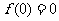
∴当 时,
时,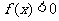
综上得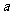 的取值范围为
的取值范围为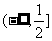
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.
(22) (本小题满分10分) 选修4-1;几何证明选讲
如图,已知圆上的弧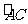 =
=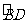 ,过C点的圆的切线与BA的延长线交于E点,证明:
,过C点的圆的切线与BA的延长线交于E点,证明:
 (Ⅰ)
(Ⅰ)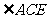 =
=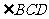 ;
;
(Ⅱ) ;
;
[答案]
解:
(I)∵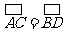
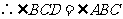
又∵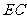 与圆相切于点
与圆相切于点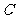 ,∴
,∴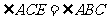
∴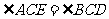
(II)∵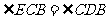 ,
,
∴△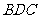 相似于△
相似于△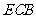
故
即 
(23) (本小题满分10分)选修4-4;坐标系与参数方程
已知直线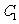 :
: (t为参数),圆
(t为参数),圆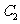 :
: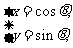 (
(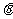 为参数),
为参数),
(Ⅰ)当 =
=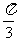 时,求
时,求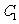 与
与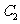 的交点坐标;
的交点坐标;
(Ⅱ)过坐标原点O作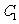 的垂线,垂足为A,P为OA的中点,当
的垂线,垂足为A,P为OA的中点,当 变化时,求P点轨迹的参数方程,并指出它是什么曲线;
变化时,求P点轨迹的参数方程,并指出它是什么曲线;
[答案]
解:
(I)当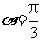 时,
时,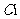 的普通方程为
的普通方程为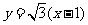 ,
, 的普通方程为
的普通方程为
联立方程组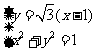
解得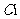 与
与 的交点为
的交点为 ,
,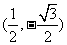
(II)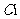 的普通方程为
的普通方程为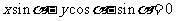
A点坐标为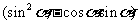
∴当 变化时,
变化时,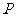 点轨迹的参数方程为
点轨迹的参数方程为
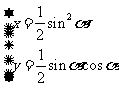 (
( 为参数)
为参数)
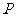 点轨迹的普通方程为
点轨迹的普通方程为
故 点轨迹是圆心为
点轨迹是圆心为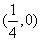 ,半径为
,半径为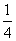 的圆
的圆
(24) (本小题满分10分)选修4-5;不等式选讲
设函数f(x)=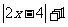
(Ⅰ)画出函数y=f(x)的图像;
(Ⅱ)若不等式f(x)≤ax的解集非空,求a的取值范围.

[答案]
解:
(I)由于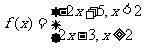
则函数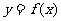 的图像如图所示
的图像如图所示
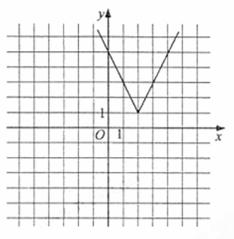
(II)由函数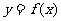 与函数
与函数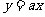 的图像可知,当且仅当
的图像可知,当且仅当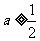 或
或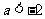 时,函数
时,函数
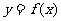 与函数
与函数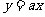 的图像有交点,故不等式
的图像有交点,故不等式 的解集非空时,
的解集非空时,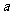 的取值范围
的取值范围
为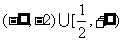
(13)
设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x) ≤1,可以用随机模拟方法近似计算积分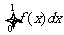 ,先产生两组(每组N个)区间[0,1]上的均匀随机数
,先产生两组(每组N个)区间[0,1]上的均匀随机数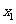 ,
, …,
…,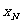 和
和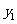 ,
,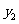 …,
…,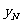 ,由此得到N个点(
,由此得到N个点(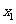 ,
,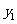 )(i=1,2,…,N),在数出其中满足
)(i=1,2,…,N),在数出其中满足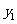 ≤
≤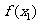 ((i=1,2,…,N))的点数
((i=1,2,…,N))的点数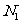 ,那么由随机模拟方法可得积分
,那么由随机模拟方法可得积分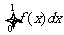 的近似值为
.
的近似值为
.
[答案]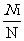
(14)正视图为一个三角形的几何体可以是 .(写出三种)
[答案]三棱柱,三棱锥,圆锥
(15)过点A(4,1)的圆C与直线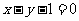 相切于点 B(2,1).则圆C的方程为
.
相切于点 B(2,1).则圆C的方程为
.
[答案]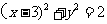
(16)在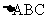 中,D为边BC上一点,BD=
中,D为边BC上一点,BD=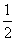 DC,
DC,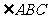 =120°,AD=2,若
=120°,AD=2,若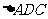 的面积为
的面积为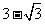 ,则
,则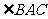 = .
= .
[答案]60°
(1)已知集合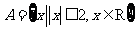 ,
, ,则
,则
(A)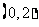 (B)
(B)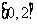 (C)
(C)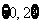 (D)
(D)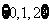
[答案]D
[解析]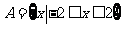 ,
, ,
,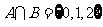
(2)已知复数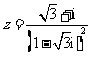 ,
, 是
是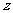 的共轭复数,则
的共轭复数,则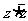
(A)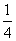 (B)
(B)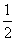 (C)1
(D)2
(C)1
(D)2
[答案]A
[解析]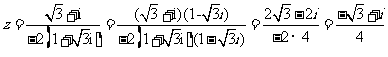
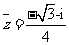 ,
,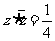
(3)曲线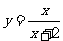 在点
在点 处的切线方程为
处的切线方程为
(A)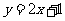 (B)
(B)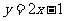 (C)
(C)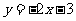 (D)
(D)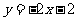
[答案]A
[解析]
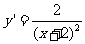 ,切线的斜率为2
,切线的斜率为2
切线方程为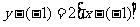 ,即
,即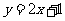 .
.
(4)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为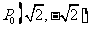 ,角速度为1,那么点P到x轴距离d关于时间t的函数图像大致为
,角速度为1,那么点P到x轴距离d关于时间t的函数图像大致为
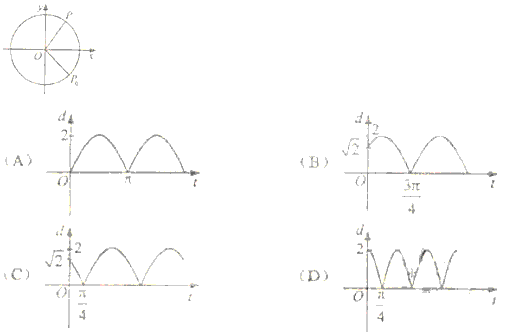
[答案]C
[解析]当点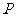 在
在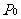 ,即
,即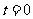 ,
,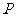 到
到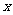 轴的距离为
轴的距离为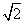 。
。
∵ ,∴
,∴
∵角速度为1,∴从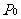 转到
转到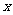 轴需要的时间为
轴需要的时间为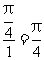 ,即当
,即当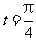 时,
时,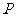 到
到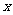 轴的距离为
轴的距离为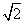
(5)已知命题
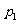 :函数
:函数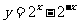 在R为增函数,
在R为增函数,
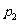 :函数
:函数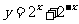 在R为减函数,
在R为减函数,
则在命题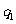 :
: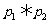 ,
,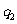 :
: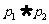 ,
,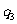 :
: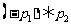 和
和 :
: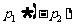 中,真命题是
中,真命题是
(A)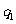 ,
,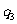 (B)
(B)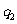 ,
,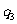 (C)
(C)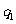 ,
, (D)
(D)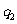 ,
,
[答案]C
[解析]∵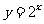 为增函数,
为增函数,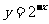 为减函数,∴
为减函数,∴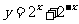 为增函数,所以
为增函数,所以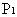 为真
为真
又∵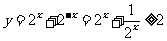 ,∴
,∴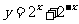 不是减函数,故
不是减函数,故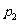 为假.
为假.
∴ 为真;
为真;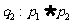 为假;
为假;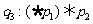 为假;
为假;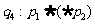 为真.
为真.
(6)某种种子每粒发芽的概率都为0.9,现播种了1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望为
(A)100 (B)200 (C)300 (D)400
[答案]B
[解析]设没有发芽的种子数为随机变量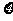 ,则
,则 ,
,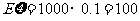 ,
,
补种的种子数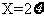 ,故
,故
(7)如果执行右面的框图,输入 ,则输出的数等于
,则输出的数等于
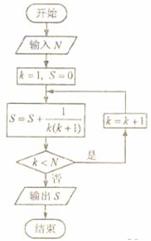
(A)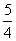 (B)
(B)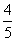
(C)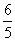 (D)
(D)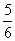
[答案]B
(8)设偶函数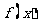 满足
满足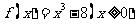 ,则
,则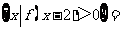
(A) (B)
(B)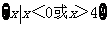
(C)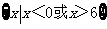 (D)
(D)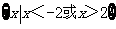
[答案]B
(9)若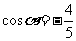 ,
, 是第三象限的角,则
是第三象限的角,则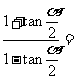
(A)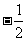 (B)
(B)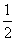 (C)2
(D)
(C)2
(D)
[答案]A
(10)设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为
(A)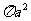 (B)
(B)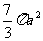 (C)
(C)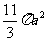 (D)
(D)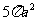
[答案]B
(11)已知函数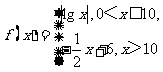 若a,b,c互不相等,且
若a,b,c互不相等,且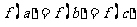 ,则abc的取值范围是
,则abc的取值范围是
(A) (B)
(B)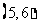 (C)
(C)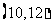 (D)
(D)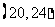
[答案]C
(12)已知双曲线E的中心为原点,F(3,0)是E的焦点,过F的直线l与E相交于A,B两点,且AB的中点为N(-12,-15),则E的方程为
(A)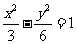 (B)
(B) 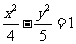 (C)
(C) 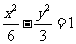 (D)
(D)
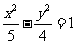
[答案]B
第Ⅱ卷
本卷包括必考题和选考题两部分。第(13)题~第(21)题为必考题,每个试题考生都必须做答。第(22)题~第(24)题为选考题,考生根据要求做答。
2.下列词语中,没有错别字的一组是
A、依稀 膨涨 戈壁滩 云蒸霞蔚
B、涵盖 阴霾 捉谜藏 烘云托月
C、贻误 甬道 交谊舞 寥若晨星
D、吆喝 绪论 擦边球 名门旺族
2.不等式 的解是_____.
的解是_____.
2010年福建省晋江市初中毕业班学业质量检查
友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况.如果你全卷得分低于90分(及格线),则本题的得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果你全卷总分已经达到或超过90分,则本题的得分不计入全卷总分.
1.若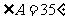 , 则
, 则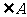 的余角等于 度.
的余角等于 度.
26.(13分)如图,在等边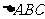 中,线段
中,线段 为
为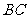 边上的中线. 动点
边上的中线. 动点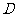 在直线
在直线 上时,以
上时,以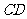 为一边且在
为一边且在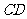 的下方作等边
的下方作等边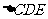 ,连结
,连结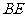 .
.
(1) 填空: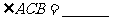 度;
度;
(2) 当点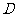 在线段
在线段 上(点
上(点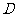 不运动到点
不运动到点 )时,试求出
)时,试求出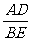 的值;
的值;
(3)若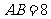 ,以点
,以点 为圆心,以5为半径作⊙
为圆心,以5为半径作⊙ 与直线
与直线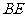 相交于点
相交于点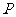 、
、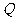 两点,在点
两点,在点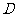 运动的过程中(点
运动的过程中(点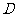 与点
与点 重合除外),试求
重合除外),试求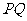 的长.
的长.
25.(13分)已知:如图,把矩形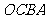 放置于直角坐标系中,
放置于直角坐标系中,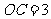 ,
,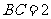 ,取
,取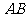 的中点
的中点 ,连结
,连结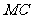 ,把
,把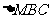 沿
沿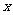 轴的负方向平移
轴的负方向平移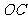 的长度后得到
的长度后得到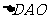 .
.
(1)试直接写出点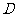 的坐标;
的坐标;
(2)已知点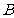 与点
与点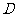 在经过原点的抛物线上,点
在经过原点的抛物线上,点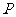 在第一象限内的该抛物线上移动,过点
在第一象限内的该抛物线上移动,过点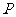 作
作 轴于点
轴于点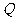 ,连结
,连结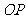 .
.
①若以 、
、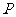 、
、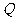 为顶点的三角形与
为顶点的三角形与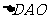 相似,试求出点
相似,试求出点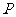 的坐标;
的坐标;
②试问在抛物线的对称轴上是否存在一点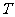 ,使得
,使得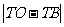 的值最大.
的值最大.

24.(10分)已知:如图,有一块含 的直角三角板
的直角三角板 的直角边长
的直角边长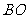 的长恰与另一块等腰直角三角板
的长恰与另一块等腰直角三角板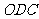 的斜边
的斜边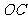 的长相等,把该套三角板放置在平面直角坐标系中,且
的长相等,把该套三角板放置在平面直角坐标系中,且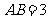 .
.
(1)若双曲线的一个分支恰好经过点 ,求双曲线的解析式;
,求双曲线的解析式;
 (2)若把含
(2)若把含 的直角三角板绕点
的直角三角板绕点 按顺时针方向旋转后,斜边
按顺时针方向旋转后,斜边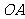 恰好与
恰好与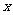 轴重叠,点
轴重叠,点 落在点
落在点 ,试求图中阴影部分的面积(结果保留
,试求图中阴影部分的面积(结果保留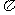 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com