
2009年7月22日千年一遇的日全食在我国长江流域发生。江苏苏州、浙江的杭州、安徽铜陵、上海等很多地方打出了“最佳观测地”的旗号,这些城市成为“日全食经济圈”。回答4-6题。
4.“最佳观测地”是指( )
A.在日全食中心线上的区域,观测时间长 B.经济发达,环境优美
C.交通、住宿非常方便
 天气晴朗,能见度高
天气晴朗,能见度高
5.“日全食”能看见的太阳大气及相对应的太阳活动是( )
A.色球 日珥
B.日冕 耀斑
C.光球 黑子  日冕 太阳风
日冕 太阳风
6.这天的月相和潮汐分别是( )
A.上弦月 小潮 B.望 大潮 C.朔 大潮
 下弦月 小潮
下弦月 小潮
2009年10月19日16时35分,中国海上搜救中心总值班室接到青岛远洋运输公司报告,该公司所属的中国籍散货轮“德新海”轮(船员25人),装载7万余吨煤,在由南非开往印度航次中遭海盗劫持,目前海盗正在此船拖往索马里据点。接到报告之后,中国海军在亚丁湾(A汇合点)的护航编队火速赶往出事地点展开营救。回答1-3题。

1.事发地点远离中国护航编队A汇合点南偏东1080海里,那么A汇合点在图中①②③④中的哪一地点( )
A.① B.②
C.③
 ④
④
2.事发地点位于两大板块交界处,该两大板块是( )
A.亚欧板块和印度洋板块,属于生长边界
B.非洲板块和印度洋板块,属于生长边界
C.亚欧板块和印度洋板块,属于消亡边界
 非洲板块和印度洋板块,属于消亡边界
非洲板块和印度洋板块,属于消亡边界
3.“德新海”轮被海盗劫持时( )
A.朝霞满天 B.可能遇到飓风 C.太阳方向接近正北  太阳方向接近正南
太阳方向接近正南
22.(本小题满分12分)设等比数列{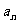 }的前
}的前 项和
项和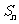 ,首项
,首项 ,公比
,公比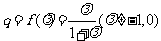 .
.
(Ⅰ)证明: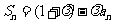 ;
;
(Ⅱ)若数列{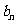 }满足
}满足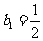 ,
,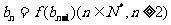 ,求数列{
,求数列{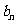 }的通项公式;
}的通项公式;
(Ⅲ)若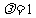 ,
,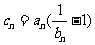 ,数列{
,数列{ }的前项和为
}的前项和为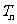 ,求证:当
,求证:当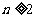 时,
时,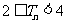 .
.
21.(本小题满分12分)已知椭圆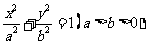 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线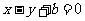 是抛物线
是抛物线 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点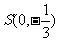 的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ?
若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ?
若存在,求点T坐标;若不存在,说明理由.
20.(本小题满分12分)已知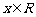 ,函数
,函数 在
在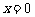 处取得极值,曲线
处取得极值,曲线 过原点
过原点 和点
和点 .若曲线
.若曲线 在点
在点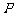 处的切线
处的切线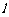 与直线
与直线 的夹角为
的夹角为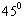 ,且直线
,且直线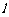 的倾斜角
的倾斜角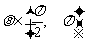
(Ⅰ)求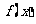 的解析式;
的解析式;
(Ⅱ)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数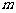 的取值范围;
的取值范围;
(Ⅲ)若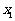 、
、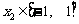 ,求证:
,求证: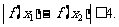
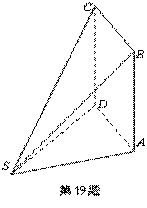
19.(本小题满分12分)如图,多面体ABCDS中,面ABCD为矩形,
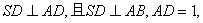
 ,
,
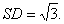
(I)求证:CD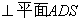 ;
;
(II)求AD与SB所成角的余弦值;
(III)求二面角A-SB-D的余弦值.
18.(本题满分12分)有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各学校做问卷调查.某中学A,B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分为:5、8、9、9、9;B班5名学生得分为:6,7,8,9,10.
(Ⅰ)请你估计A,B两个班中哪个班的问卷得分要稳定一些;
(Ⅱ)如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率.
17.(本小题满分10分)已知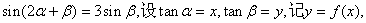
(Ⅰ)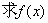 的解析表达式;
的解析表达式;
(Ⅱ)若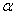 角是一个三角形的最小内角,试求函数
角是一个三角形的最小内角,试求函数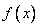 的值域.
的值域.
16.给出下列命题:
A.函数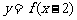 和
和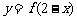 的图象关于直线
的图象关于直线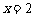 对称.
对称.
B.已知函数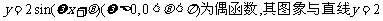 的交点的横坐标为
的交点的横坐标为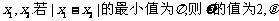 的值为
的值为 .
.
C.底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
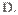 若
若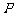 为双曲线
为双曲线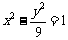 上的一点,
上的一点,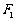 、
、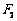 分别为双曲线的左右焦点,且
分别为双曲线的左右焦点,且 ,则
,则 或
或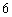 .
.
其中k_s_5_u正确的命题是 (把所有k_s_5_u正确的命题的选项都填上)
15.写出“函数f (x)=x2+2ax+1(a∈R)在区间(1,+∞)上是增函数”成立的一个充分不必要条件:_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com