
22. (示范性高中做)
解:(I)由已知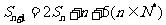 可得
可得 两式相减得
两式相减得
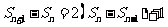 即
即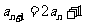 从而
从而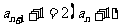 当
当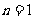 时
时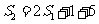 所以
所以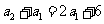 又
又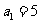 所以
所以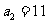 从而
从而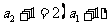
故总有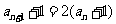 ,
,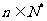 又
又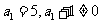 从而
从而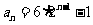 ;…………6分
;…………6分
(II)由(I)知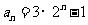
因为 =
=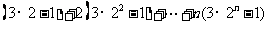
=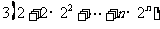 -
- =
=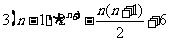 ……………12分
……………12分
22.(普通高中做)
解:(Ⅰ)由已知得
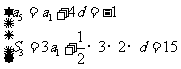 ……………………………………2分
……………………………………2分
解得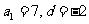 ………………………………………………4分
………………………………………………4分
则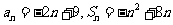 ……………………………………6分
……………………………………6分
(Ⅱ)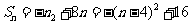
当 时前
时前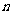 项和最大,最大值为16…………………………12分
项和最大,最大值为16…………………………12分
21.解:(Ⅰ)依题意可设A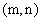 、
、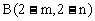 ,则
,则
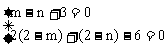 ,
, 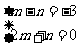 ,解得
,解得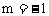 ,
,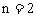 .
…………4分
.
…………4分
即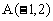 ,又l过点P
,又l过点P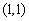 ,易得AB方程为
,易得AB方程为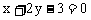 .………………6分
.………………6分
(Ⅱ)设圆的半径为R,则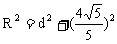 ,其中d为弦心距,
,其中d为弦心距,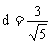 ,可得
,可得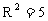 ,故所求圆的方程为
,故所求圆的方程为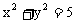 .………………12分
.………………12分
20. (普通高中做)解:
(普通高中做)解:
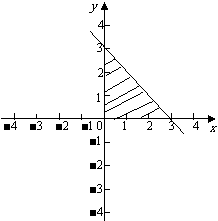
不等式组表示的平面区域如图所示.
阴影部分是一个直角三角形.------6分
目标函数变形为

当上面的直线经过可行域上的点(0,3)时,截距
最大,z最大, ------12分
------12分
 20
20 (示范性高中做) 解:设公司在甲、乙两个仓储基地储存的原材料分别为
(示范性高中做) 解:设公司在甲、乙两个仓储基地储存的原材料分别为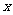 吨和
吨和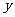 吨,总收益为
吨,总收益为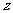 元,由题意得
元,由题意得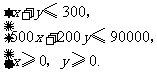
目标函数为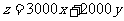
 ……………4分
……………4分
二元一次不等式组等价于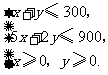
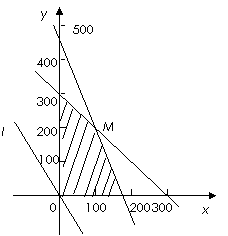
作出二元一次不等式组所表示的平面区域.
如图:
作直线 ,
,
即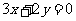

平移直线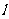 ,从图中可知,当直线
,从图中可知,当直线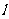 过
过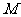 点时,
点时,
目标函数取得最大值 ……………8分
……………8分
联立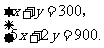 解得
解得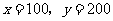

 点
点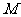 的坐标为
的坐标为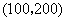

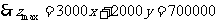 (元)……………12分
(元)……………12分
19.
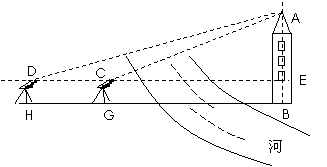 解: 如图,测出
解: 如图,测出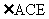 的度数,测出
的度数,测出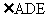 的度数,测量出HG的长度. 即可计算出建筑物的高度AB. ……………6分
的度数,测量出HG的长度. 即可计算出建筑物的高度AB. ……………6分
理由如下:
设: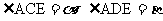 ,HG=s.在
,HG=s.在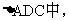 由正弦定理得
由正弦定理得
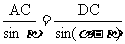 ,所以
,所以 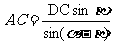 .
.
在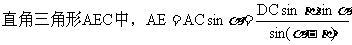
建筑物的高AB=EB+AE= 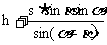 ……………12分
……………12分
18.(方案一)解: 与
与 垂直
垂直

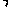


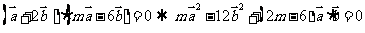

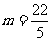 …………12分
…………12分
( 方案二 )
解:(Ⅰ)俯视图------6分
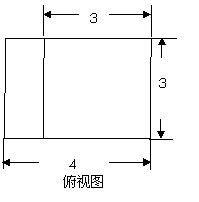 (Ⅱ)(普通高中做)
(Ⅱ)(普通高中做) 由已知易知
由已知易知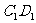 是三棱锥
是三棱锥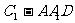 的高
的高
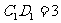 ,
,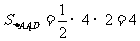
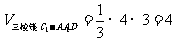 ( cm3 ) ……12分
( cm3 ) ……12分
(示范性高中做)
由题意知所求的多面体是以点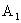 为顶点,
为顶点,
以四边形ABCD为底面的四棱锥.
易知四边形ABCD是矩形.AB=3,
AD=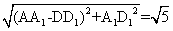 ---------8分
---------8分
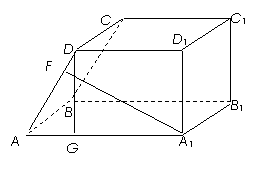

过点D作DG⊥AG
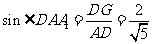

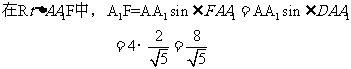
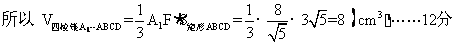
17. 解:不等式可化为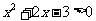 ……………3分
……………3分
方程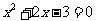 有两个实数根
有两个实数根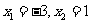 ,……………6分
,……………6分
所以不等式的解集为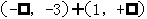 ……………10分
……………10分
13.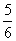 ; 14.
; 14. 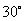 ,2 ; 15. 1023; 16. 2
,2 ; 15. 1023; 16. 2
1---3. CAC 4 . B (D) ; 5.B ; 6 . D ; 7. B (C); 8---12. ACCDB
22.(本小题满分12分)
(普通高中做)
已知等差数列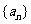 中,
中,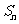 为
为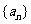 的前
的前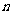 项和,
项和,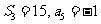 .
.
(Ⅰ)求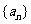 的通项
的通项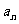 与
与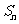 ;
;
(Ⅱ)当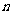 为何值时,
为何值时,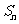 为最大?最大值为多少?
为最大?最大值为多少?
(示范性高中做)
已知数列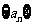 的首项
的首项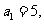 前
前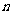 项和为
项和为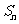 ,且
,且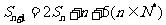
(Ⅰ)求数列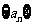 的通项公式;
的通项公式;
(Ⅱ)令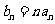 ,求数列
,求数列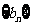 的前n项和
的前n项和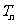 .
.
2009-2010年第二学期高一数学答案及评分标准 6.26
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com