
21. (本题12分)
设奇函数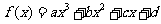 的图像在点
的图像在点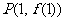 处切线的斜率等于
处切线的斜率等于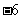 ,又
,又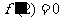 .
.
(1)求函数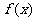 的解析式;
的解析式;
(2)设函数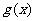 的导函数
的导函数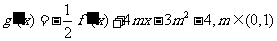 ,
,
求函数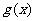 的单调区间.
的单调区间.
20. (本题12分)
在中央电视台所举办的北京2008年奥运火炬手的一期选拔节目中,假定每个选手需要进行四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰。若某选手能正确回答第一、二、三、四轮问题的概率分别是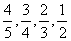 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手进入第四轮才被淘汰的概率;
(2)该选手在选拔过程中,他回答过的问题的总个数记为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
19. (本题12分)
已知数列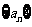 的通项公式
的通项公式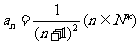 ,
,
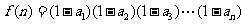 ,
,
试求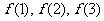 的值,由此推测
的值,由此推测 的计算公式,并用数学归纳法加以证明.
的计算公式,并用数学归纳法加以证明.
18. (本题12分)
已知函数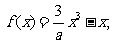 其中(
其中(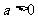 ).
).
(1)求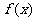 的单调增区间;
的单调增区间;
(2)曲线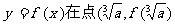 )处的切线恒过y轴上一个定点,求此定点坐标.
)处的切线恒过y轴上一个定点,求此定点坐标.
17. (本题10分)
已知函数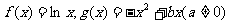 ,若函数
,若函数 在其定义域内是增函数,求
在其定义域内是增函数,求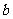 的取值范围.
的取值范围.
16. 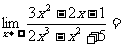 .
.
15.在四个数的两旁各加一条竖线,引进符号: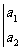
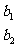
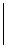 ,定义
,定义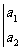
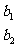
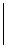 =
= ,则函数
,则函数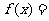
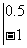
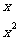
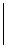 在
在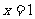 处切线的斜率为
.
处切线的斜率为
.
14. 随机变量
 ,
, ,则
,则 .
.
13. 若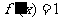 ,则
,则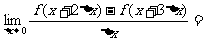 .
.
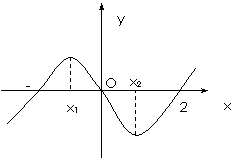
12. 如图所示曲线是函数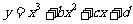 的大致图象,则
的大致图象,则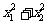 等于(
)
等于(
)
A.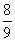 B.
B. 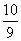 C.
C.
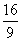 D.
D. 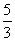
卷Ⅱ(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com