
22.(本题满分18分,第(1)小题9分,第(2)小题9分)
解:(1)方法1:①当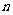 为奇数时,
为奇数时,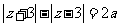 ,常数
,常数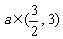 ,
,
轨迹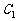 为双曲线,其方程为
为双曲线,其方程为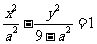 ;……3分
;……3分
②当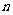 为偶数时,
为偶数时,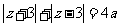 ,常数
,常数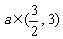 ,
,
轨迹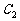 为椭圆,其方程为
为椭圆,其方程为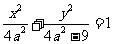 ;……6分
;……6分
依题意得方程组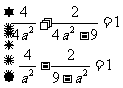
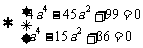 解得
解得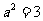 ,
,
因为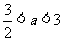 ,所以
,所以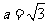 ,
,
此时轨迹为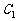 与
与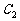 的方程分别是:
的方程分别是: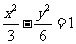
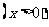 ,
,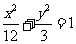 .……9分
.……9分
方法2:依题意得
 ……3分
……3分
轨迹为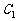 与
与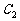 都经过点
都经过点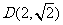 ,且点
,且点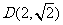 对应的复数
对应的复数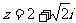 ,
,
代入上式得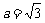 ,……6分
,……6分

设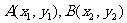 ,则
,则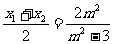
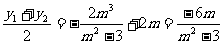
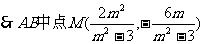 ……10分
……10分
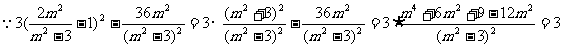
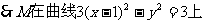 ……12分
……12分
(3)设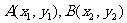 设存在实数
设存在实数 ,使
,使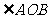 为锐角,
为锐角,
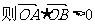
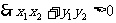 ……14分
……14分
因为 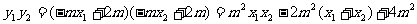
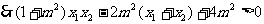 ……16分
……16分
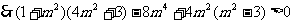 即
即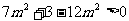
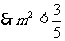 ,与
,与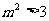 矛盾
矛盾 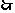 不存在……18分
不存在……18分
 于是由图形不难得到
于是由图形不难得到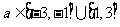 ,……12分
,……12分
故两个命题同时为真的实数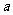 的取值范围是
的取值范围是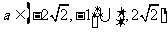 .……14分
.……14分
21.(本题满分16分,第(1)小题6分,第(2)小题10分)
解:(1)如图所示,建立平面直角坐标系……2分
由题意得,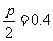 ……4分
……4分
所以,抛物线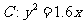 ……6分
……6分
(2)设抛物线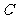 的焦点为
的焦点为 由题意得,
由题意得,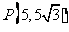 ……8分
……8分
根据抛物线的定义知,公路总长 ……12分
……12分
当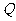 为线段
为线段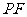 与抛物线
与抛物线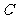 的交点(如图)时,公路总长最小,
的交点(如图)时,公路总长最小,
最小值为9.806千米……16分
23.(本题满分18分,第(1)小题4分,第(2)小题8分,第(3)小题6分)
已知双曲线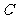 :
: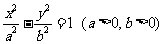 的一个焦点是
的一个焦点是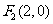 ,且
,且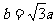 .
.
(1)求双曲线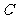 的方程;
的方程;
(2)设经过焦点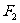 的直线
的直线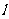 的一个法向量为
的一个法向量为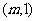 ,当直线
,当直线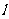 与双曲线
与双曲线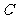 的右支相交于不同的两点
的右支相交于不同的两点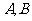 时,求实数
时,求实数 的取值范围;并证明
的取值范围;并证明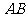 中点
中点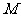 在曲线
在曲线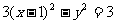 上.
上.
(3)设(2)中直线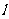 与双曲线
与双曲线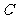 的右支相交于
的右支相交于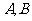 两点,问是否存在实数
两点,问是否存在实数 ,使得
,使得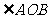 为锐角?若存在,请求出
为锐角?若存在,请求出 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
2009学年第二学期测试答案 高二年级
22.(本题满分18分,第(1)小题9分,第(2)小题9分)
设复数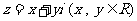 与复平面上点
与复平面上点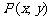 对应.
对应.
(1)设复数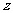 满足条件
满足条件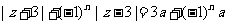 (其中
(其中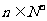 ,常数
,常数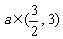 ),当
),当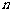 为奇数时,动点
为奇数时,动点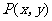 的轨迹为
的轨迹为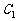 ;当
;当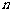 为偶数时,动点
为偶数时,动点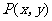 的轨迹为
的轨迹为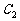 ,且两条曲线都经过点
,且两条曲线都经过点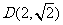 ,求轨迹
,求轨迹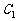 与
与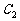 的方程;
的方程;
(2)在(1)的条件下,轨迹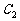 上存在点
上存在点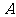 ,使点
,使点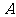 与点
与点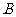
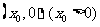 的最小距离不小于
的最小距离不小于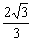 ,求实数
,求实数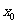 的取值范围.
的取值范围.
21.(本题满分16分,第(1)小题6分,第(2)小题10分)
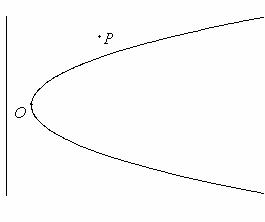
如图,弯曲的河流是近似的抛物线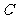 ,公路
,公路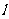 恰好是
恰好是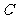 的准线,
的准线,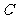 上的点
上的点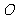 到
到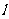 的距离最近,且为
的距离最近,且为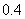 千米,城镇
千米,城镇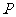 位于点
位于点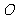 的北偏东
的北偏东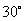 处,
处,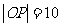 千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路
千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路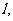 以便建立水陆交通网.
以便建立水陆交通网.
(1)建立适当的坐标系,求抛物线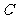 的方程;
的方程;
(2)为了降低修路成本,必须使修建的两条公路总长最小,请给出修建方案(作出图形,在图中标出此时码头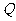 的位置),并求公路总长的最小值(精确到0.001千米)
的位置),并求公路总长的最小值(精确到0.001千米)
20.(本题满分14分)
已知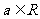 ,且以下命题都为真命题:
,且以下命题都为真命题:
命题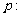 实系数一元二次方程
实系数一元二次方程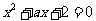 的两根都是虚数;
的两根都是虚数;
命题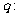 存在复数
存在复数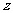 同时满足
同时满足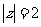 且
且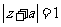 .
.
求实数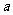 的取值范围.
的取值范围.
19.(本题满分12分,第(1)小题6分,第(2)小题6分)
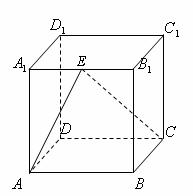
如图,在棱长为1的正方体中,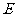 是棱
是棱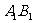 的中点,
的中点,
(1)求证: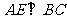 ;
;
(2)求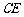 与平面
与平面 所成角大小(用反三角函数表示).
所成角大小(用反三角函数表示).
18.已知直线 、
、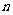 及平面
及平面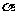 ,其中m∥n,那么在平面
,其中m∥n,那么在平面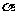 内到两条直线
内到两条直线 、
、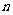 距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集.其中正确的是( )
距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集.其中正确的是( )
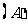 (1)(2)(3)
(1)(2)(3) 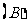 (1)(4)
(1)(4)  (1)(2)(4)
(1)(2)(4)  (2)(4)
(2)(4)
17.在复平面内,若复数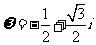 对应的向量为
对应的向量为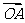 ,复数
,复数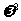 对应的向量为
对应的向量为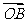 ,则向量
,则向量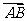 对应的复数是( )
对应的复数是( )
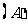 1
1
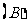
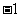
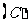
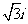
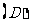
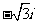
16.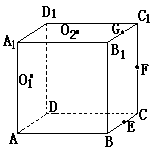 如图,正方体
如图,正方体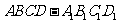 中,若
中,若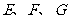 分别为棱
分别为棱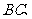
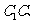
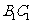 的中点,
的中点,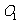 、
、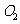 分别为四边形
分别为四边形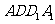 、
、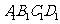 的中心,则下列各组中的四个点不在同一个平面上的是( )
的中心,则下列各组中的四个点不在同一个平面上的是( )
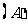
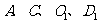
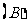
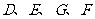
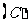
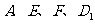
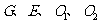
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com