
20.(本题12分)七个人排成两排照相,前排3人,后排4人.
(1) 求甲在前排,乙在后排的概率;
(2) 求甲、乙在同一排且相邻的概率;
(3) 求甲、乙之间恰好有一人的概率.
19.(本题12分)已知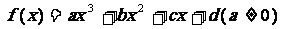 是定义在R上
是定义在R上
的函数, 且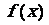 在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
有相反的单调性.
(1) 求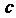 的值;
的值;
(2) 在函数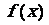 的图象上是否存在一点
的图象上是否存在一点 ,使得
,使得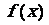 在点
在点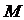 的
的
切线斜率为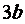 ?若存在,求出点
?若存在,求出点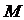 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
18. (本题12分) 设函数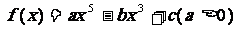 .
.
(1)若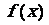 在
在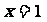 和
和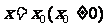 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,
极小值为1,求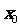 及实数
及实数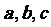 的值;
的值;
(2) 若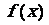 在
在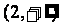 上单调递增且
上单调递增且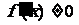 ,求
,求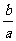 的最大值.
的最大值.
17.(本题10分) 在等比数列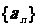 中,
中,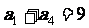 ,
,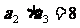 ,
,
求数列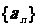 的前6项和
的前6项和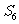 .
.
16.函数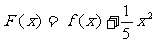 的图象在点
的图象在点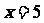 处的切线方程是
处的切线方程是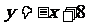 ,
,
则 的值等于
的值等于
15.从1,2,3,…,10这十个数中,任取3个不同的数,则这3个数恰好能组成
等差数列的概率为
14.设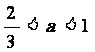 ,函数
,函数 的最大值为1,最小值为
的最大值为1,最小值为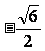 ,则常数
,则常数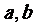 的值分别为
和
的值分别为
和
13.甲、乙两人自相距30米处同时相向运动,甲每分钟走3米;乙第1分钟走2米,
且以后每分钟比前1分钟多走0.5米,则甲和乙开始运动后 分钟相遇.
12.设函数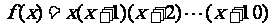 ,则
,则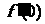 的值为( )
的值为( )
A.10 B.55 C. 10! D.0
11.函数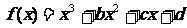 在区间
在区间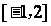 上是减函数,那么
上是减函数,那么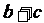 有( )
有( )
A.最大值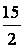 B.最大值
B.最大值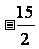 C.最小值
C.最小值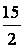 D.最小值
D.最小值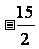
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com