
6. 取一根长度为6 m的绳子,拉直后在任意位置剪断,那么剪得两段绳子的长都不小于2 m的概率是
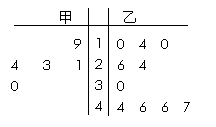 A.
A. 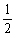 B.
B. 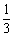 C.
C.
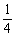 D.
D.
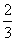
5. 已知集合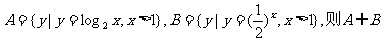 等于
等于
A. 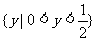 B.
B. 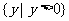 C.
C. 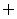 D.
D.
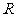
4. 已知直线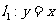 ,若直线
,若直线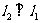 ,则直线
,则直线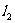 的倾斜角为
的倾斜角为
A. 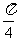 B.
B.
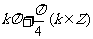 C.
C. 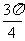 D.
D.
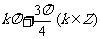
3. 已知等差数列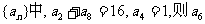 的值为
的值为
A. 15 B. 17 C. 36 D. 64
2.“x = 2且y = – 2”是“xy = – 4”的
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不必要也不充分条件
项是符合题目要求的。
1.
复数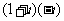 等于
等于
A.
 B.
B.
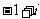 C.
C.
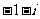 D.
D. 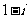
22.(本小题满分14分)函数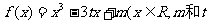 为常数)是奇函数.
为常数)是奇函数.
(1)若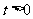 ,求函数
,求函数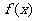 的图象与横轴的交点坐标.
的图象与横轴的交点坐标.
(2)设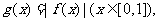 试求
试求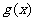 的最大值F(t);
的最大值F(t);
(3)求F(t)的最小值.








21.(本小题满分12分)设向量a=(x+1,y),b=(x-1,y),点P(x,y)为动点,已知|a|+|b|=4.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P的轨迹与x轴负半轴交于点A,过点F(1,0)的直线交点P的轨迹于B、C两点,试推断△ABC的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由.
20.(本小题满分12分)已知数列{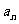 }中
}中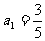 ,
, (n≥2,
(n≥2, ),数列
),数列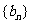 ,满足
,满足 (
( )
)
(1)求证数列{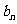 }是等差数列;
}是等差数列;
(2)若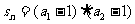 +
+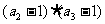 +
+
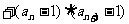
是否存在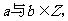 使得:
使得: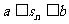 恒成立.若有,求出
恒成立.若有,求出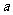 的最大值与
的最大值与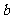 的最小值,如果没有,请说明理由.
的最小值,如果没有,请说明理由.
19. (本小题满分12分)如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
(本小题满分12分)如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
(1)求证:AF⊥BD;
(2)求二面角A―BD―E的正弦值.
k*s*5*u
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com