
19.(本小题满分12分)
已知函数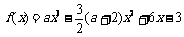 .
.
(1)当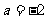 时,求函数
时,求函数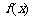 的单调区间和极值;
的单调区间和极值;
(2)当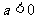 时,试求方程
时,试求方程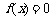 根的个数.
根的个数.
18.(本小题满分12分)
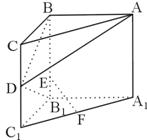 如图,在直三棱柱
如图,在直三棱柱 中,
中, ,
,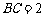 ,
,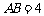 ,
,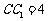 ,E在
,E在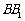 上,且
上,且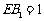 ,
,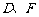 分别为
分别为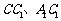 的中点.
的中点.
(1)求证: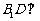 平面
平面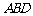 ;
;
(2)求异面直线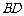 与
与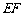 所成的角;
所成的角;
(3)求点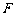 到平面
到平面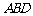 的距离.
的距离.
17.(本小题满分12分)
要建造一个容积为2000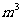 ,深为5
,深为5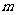 的长方体无盖蓄水池,池壁的造价为95
的长方体无盖蓄水池,池壁的造价为95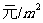 ,池底的造价为135
,池底的造价为135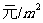 ,若水池底的一边长为
,若水池底的一边长为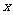
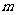 ,水池的总造价为
,水池的总造价为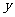 元。
元。
(1)把水池总造价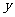
 表示为
表示为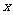 的函数。
的函数。
(2)当水池 的长
的长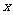 为多少时,水池的总造价最少?
为多少时,水池的总造价最少?
16.(本小题满分12分)
在△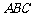 中,角
中,角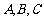 所对边分别为
所对边分别为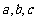 ,且
,且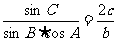 .
.
(1)求角A;(2)若
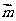
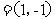 ,
,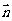 =
= ,,试求
,,试求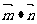 的取值范围.
的取值范围.
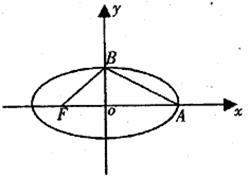
15.如下图,椭圆中心在坐标原点,焦点在坐标轴上,A、B是顶点,F是左焦点;当BF⊥AB时,此类椭圆称为 “黄金椭圆”,其离心率为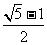 。类比“黄金椭圆”可推算出“黄金双曲线”的离心率e=
。
。类比“黄金椭圆”可推算出“黄金双曲线”的离心率e=
。
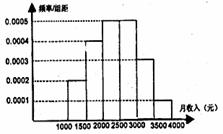
13.一个社会调查机构就某地居民的月收入
调查了10000人,并根据所得数据画
了样本的频率分布直方图(如下图)。
为了分析居民的收入与年龄、学历、
职业等方面的关系,要从这10000人
中再用分层抽样方法抽出100人作进一步调查,则在 (元)/
(元)/
月收入应抽出
人。 
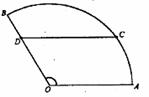 14.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,
14.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,
C是该小区的一个出入口,且小区里有一条平行 于AO的
于AO的 小
小
路CD。已 知某人从O沿OD走到D用了2分钟,从D沿着
知某人从O沿OD走到D用了2分钟,从D沿着
DC走到C用了3分钟。若此人步行的速度为每分钟50米,
则该扇形的半径为 米。
11.等差数列的前n项和为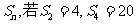 ,则该数列的公差d= 。
,则该数列的公差d= 。
 12.若
12.若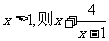 的最小值为
。
的最小值为
。
10.在实 数的原有运算法则中,我们补充定义新运算“
数的原有运算法则中,我们补充定义新运算“ ”如下:当
”如下:当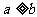 时,
时,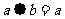 ;
;
当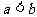
 时,
时,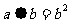 。则函数
。则函数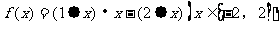 的最大值等于(“·”和“-”仍为通常的乘法和减法)
的最大值等于(“·”和“-”仍为通常的乘法和减法)  ( )
( )
A.  B. 1 C. 6 D. 12
B. 1 C. 6 D. 12
9.设A、B为双曲线 =1同一条渐近线上的两个不同的点,若|AB|=6,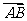 在向量
在向量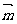 =(1,0)上的投影为
=(1,0)上的投影为 3,则双曲线的离心率e等于 ( )
3,则双曲线的离心率e等于 ( )
A.2 B.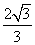 C.2或
C.2或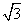 D.2或
D.2或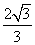
8.若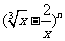 展开式中含
展开式中含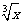 的项是第8项,则展开式含
的项是第8项,则展开式含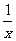 的项是 ( )
的项是 ( )
A .第8项 B.第9项 C.第10项
D.第11项
.第8项 B.第9项 C.第10项
D.第11项
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com