
3.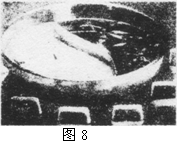
 “鸳鸯火锅”是用金属片将锅的内部空间隔成相等的两部分,一边放清汤卤,一边放红汤卤,清汤和红汤的质量、主要成分以及初温几乎相同,但是清汤卤一侧液面没有油层,红汤卤一侧液面有一层麻辣风味的泊,如图8所示。但小新注意到每次使用这种“鸳鸯火锅”吃烫涮食品时,总是红汤卤一侧首先沸腾。最初,小新认为这是由于红汤卤一侧的火更大些,但观察发现,两边的火焰相同。原来麻辣风味一侧的汤面上油层
(填“加快”或“减缓”)了汤卤的 (填物态变化名称),减少了热量的散失,所以总是红汤卤一侧先沸腾。
“鸳鸯火锅”是用金属片将锅的内部空间隔成相等的两部分,一边放清汤卤,一边放红汤卤,清汤和红汤的质量、主要成分以及初温几乎相同,但是清汤卤一侧液面没有油层,红汤卤一侧液面有一层麻辣风味的泊,如图8所示。但小新注意到每次使用这种“鸳鸯火锅”吃烫涮食品时,总是红汤卤一侧首先沸腾。最初,小新认为这是由于红汤卤一侧的火更大些,但观察发现,两边的火焰相同。原来麻辣风味一侧的汤面上油层
(填“加快”或“减缓”)了汤卤的 (填物态变化名称),减少了热量的散失,所以总是红汤卤一侧先沸腾。
2.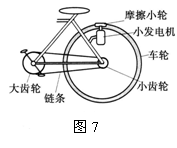 自行车后架上装有向车头灯供电的小发电机,小发电机的上端有一个摩擦小轮。行驶过程中,当需要小发电机向车头灯供电时,小轮压紧车轮,如图7所示,此时小轮在自行车车轮 力的作用下转动,发电机发电,其原理是
,
能转化成
能。
自行车后架上装有向车头灯供电的小发电机,小发电机的上端有一个摩擦小轮。行驶过程中,当需要小发电机向车头灯供电时,小轮压紧车轮,如图7所示,此时小轮在自行车车轮 力的作用下转动,发电机发电,其原理是
,
能转化成
能。
1. 2010年4月14日7时49分,我国青海省玉树藏族自治州玉树县发生了里氏7.1级地震,为及时了解震区的受灾情况,便于指挥调度,相关部门利用了飞机航拍和卫星遥感技术。飞机航拍只能在白天进行,利用的是地面物体反射的可见光来拍摄。拍摄时,地面上的物体在摄像机上成的像,应位于摄像机镜头的一倍焦距至二倍焦跟之间,且更靠近 (选填“一倍焦距”或“二倍焦距”)处;而卫星遥感则可以昼夜不停的工作,因为它不仅可以感知可见光,还可以感知物体发出的 (选填“紫外线”或“红外线”)。
23.(本题满分18分;第(1)小题4分,第(2)小题6分,第(3)小题8分)
设数列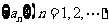 是等差数列,且公差为
是等差数列,且公差为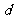 ,若数列
,若数列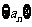 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)若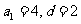 ,判断该数列是否为“封闭数列”,并说明理由?
,判断该数列是否为“封闭数列”,并说明理由?
(2)设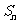 是数列
是数列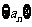 的前
的前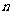 项和,若公差
项和,若公差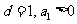 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求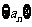 的通项公式,若不存在,说明理由;
的通项公式,若不存在,说明理由;
(3)试问:数列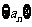 为“封闭数列”的充要条件是什么?给出你的结论并加以证明.
为“封闭数列”的充要条件是什么?给出你的结论并加以证明.
2009学年第二学期徐汇区高三年级数学学科
学 习 能 力 诊 断 卷
22.(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设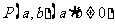 、
、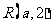 为坐标平面
为坐标平面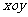 上的点,直线
上的点,直线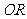 (
(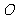 为坐标原点)与抛物线
为坐标原点)与抛物线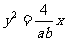 交于点
交于点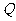 (异于
(异于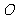 ).
).
(1) 若对任意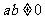 ,点
,点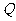 在抛物线
在抛物线 上,试问当
上,试问当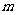 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2) 若点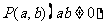 在椭圆
在椭圆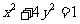 上,试问:点
上,试问:点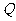 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3) 对(1)中点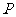 所在圆方程
所在圆方程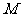 ,设
,设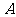 、
、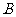 是圆
是圆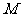 上两点,且满足
上两点,且满足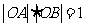 ,试问:是否存在一个定圆
,试问:是否存在一个定圆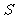 ,使直线
,使直线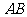 恒与圆
恒与圆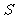 相切.
相切.
21.(本题满分16分;第(1)小题5分,第(2)小题5分,第三小题6分)
已知函数 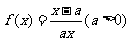
(1)判断并证明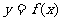 在
在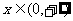 上的单调性;
上的单调性;
(2)若存在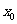 ,使
,使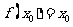 ,则称
,则称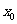 为函数
为函数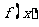 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求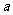 的值,并求出不动点
的值,并求出不动点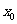 ;
;
(3)若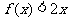 在
在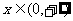 上恒成立 , 求
上恒成立 , 求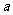 的取值范围.
的取值范围.
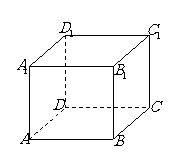
20.(本题满分14分)
(如图)已知正方体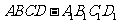 的棱长均为1,
的棱长均为1,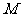 为棱
为棱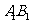 上的点,
上的点,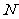 为棱
为棱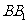 的中点,异面直线
的中点,异面直线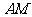 与
与 所成角的大小为
所成角的大小为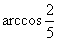 ,求
,求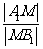 的值.
的值.
19.(本题满分14分)
在 中,
中,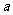 、
、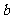 、
、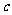 是
是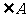 、
、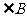 、
、 的对边,已知
的对边,已知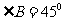 ,
,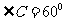 ,
,
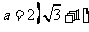 ,求
,求 的面积
的面积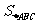 .
.
18. 已知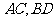 为圆
为圆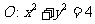 的两条互相垂直的弦,
的两条互相垂直的弦,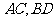 交于点
交于点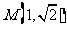 ,则四边形
,则四边形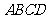 面积的最大值为----------------------------------------------------------------( )
面积的最大值为----------------------------------------------------------------( )
A 4 B 5 C 6 D 7
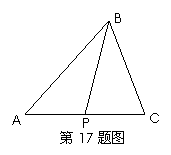
17.设P是△ABC所在平面内的一点,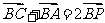 ,则----------------------------( )
,则----------------------------( )
 A.
A.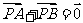 B.
B. 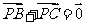 C.
C. 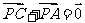 D.
D.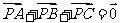
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com