
(15)(本小题满分13分)
设函数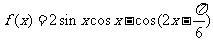 .
.
(Ⅰ)求函数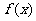 的最小正周期;
的最小正周期;
(Ⅱ)当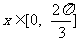 时,求函数
时,求函数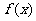 的最大值及取得最大值时的
的最大值及取得最大值时的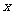 的值.
的值.
(16)(本小题满分13分)
袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取1个球,求取出1个红球2个黑球的概率;
(Ⅱ)若无放回地取3次,每次取1个球,
①求在前2次都取出红球的条件下,第3次取出黑球的概率;
②求取出的红球数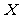 的分布列和均值(即数学期望).
的分布列和均值(即数学期望).
(17)(本小题满分14分)
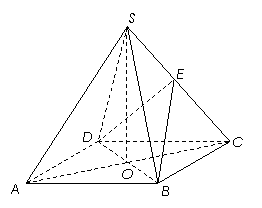 如图,在四棱锥
如图,在四棱锥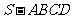 中,底面
中,底面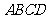 是正方形,其他四个侧面都是等边三角
是正方形,其他四个侧面都是等边三角
形,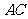 与
与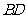 的交点为
的交点为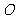 ,
,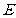 为侧棱
为侧棱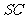 上一点.
上一点.
(Ⅰ)当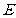 为侧棱
为侧棱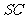 的中点时,求证:
的中点时,求证: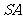 ∥平面
∥平面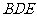 ;
;
(Ⅱ)求证:平面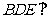 平面
平面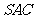 ;
;
(Ⅲ)当二面角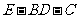 的大小为
的大小为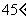 时,
时,
试判断点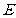 在
在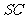 上的位置,并说明理由.
上的位置,并说明理由.
(18)(本小题满分13分)
已知函数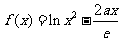 ,(
,(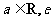 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求函数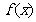 的递增区间;
的递增区间;
(Ⅱ)当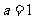 时,过点
时,过点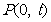
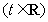 作曲线
作曲线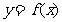 的两条切线,设两切点为
的两条切线,设两切点为
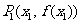 ,
,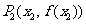
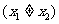 ,求证:
,求证: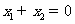 .
.
(19)(本小题满分13分)
已知动点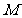 到点
到点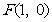 的距离,等于它到直线
的距离,等于它到直线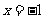 的距离.
的距离.
(Ⅰ)求点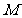 的轨迹
的轨迹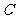 的方程;
的方程;
(Ⅱ)过点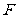 任意作互相垂直的两条直线
任意作互相垂直的两条直线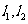 ,分别交曲线
,分别交曲线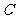 于点
于点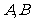 和
和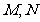 .设线段
.设线段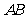 ,
,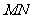 的中点分别为
的中点分别为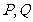 ,求证:直线
,求证:直线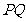 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求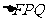 面积的最小值.
面积的最小值.
(20)(本小题满分14分)
已知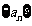 是递增数列,其前
是递增数列,其前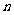 项和为
项和为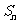 ,
,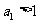 ,且
,且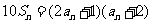 ,
,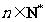 .
.
(Ⅰ)求数列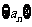 的通项
的通项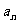 ;
;
(Ⅱ)是否存在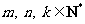 ,使得
,使得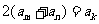 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的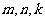 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)设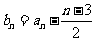 ,
,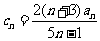 ,若对于任意的
,若对于任意的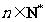 ,不等式
,不等式
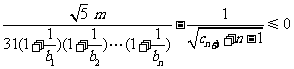 恒成立,求正整数
恒成立,求正整数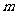 的最大值.
的最大值.
(9)不等式组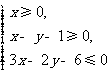 所表示的平面区域的面积等于
.
所表示的平面区域的面积等于
.
 (10)已知圆
(10)已知圆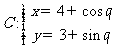 (
(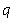 为参数),直线
为参数),直线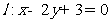 ,则圆心
,则圆心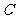 到直线
到直线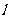 的距离为
.
的距离为
.
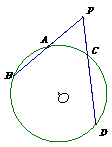
(11)如右图,从圆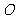 外一点
外一点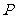 引两条直线分别交圆
引两条直线分别交圆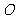 于点
于点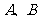 ,
,
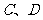 ,且
,且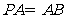 ,
, ,
,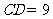 ,则
,则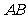 的长等
的长等
于 .
(12)如果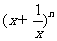 展开式中,第四项与第六项的系数相等,则
展开式中,第四项与第六项的系数相等,则
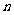 = ,展开式中的常数项的值等于
.
= ,展开式中的常数项的值等于
.
(13)上海世博园中的世博轴是一条1000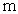 长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为
长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为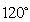 . 据此数据计算,中国馆到世博轴其中一端的距离是
. 据此数据计算,中国馆到世博轴其中一端的距离是
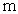 .
.

(14)已知数列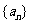 为等差数列,若
为等差数列,若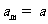 ,
,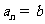 (
(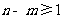 ,
,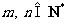 ),则
),则
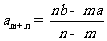 . 类比等差数列
. 类比等差数列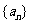 的上述结论,对于等比数列
的上述结论,对于等比数列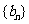 (
(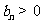 ,
,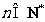 )若
)若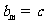 ,
,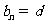 (
(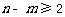 ,
,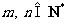 ),则可以得到
),则可以得到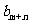 =
.
=
.
(1)已知集合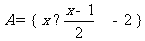 ,
,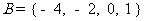 ,则
,则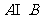 等于
等于
(A)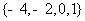 (B)
(B) (C)
(C) (D)
(D)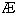
(2)已知向量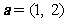 ,
,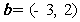 ,如果
,如果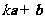 与
与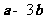 垂直,那么实数
垂直,那么实数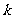 的值为
的值为
(A)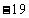 (B)
(B)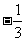 (C)
(C)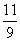 (D)
(D)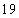
(3)一个几何体的三视图如图所示,则此几何体的体积是
(A) (B)
(B)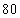 (C)
(C)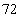 (D)
(D)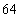

(4)某程序框图如图所示,该程序运行后,输出的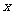 值为31,则
值为31,则 等于
等于
(A)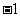 (B)
(B)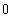 (C)
(C)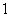 (D)
(D)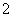
(5)已知平面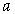 ,
,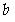 ,直线
,直线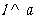 ,直线
,直线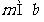 ,有下面四个命题:
,有下面四个命题:
①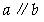
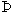
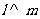 ②
② 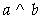
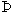
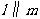
③ 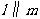
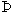
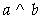 ④
④ 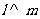
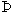
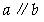 其中正确的命题是
(A)①与②
(B)③与④ (C)①与③ (D)②与④
其中正确的命题是
(A)①与②
(B)③与④ (C)①与③ (D)②与④
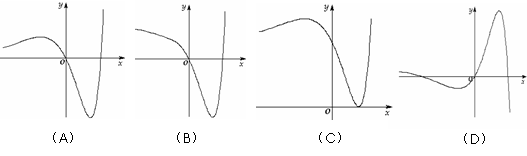
(6)函数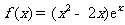 的图象大致是
的图象大致是
(7)已知椭圆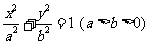 ,
,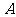 是椭圆长轴的一个端点,
是椭圆长轴的一个端点,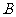 是椭圆短轴的一个端点,
是椭圆短轴的一个端点,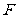 为椭圆的一个焦点. 若
为椭圆的一个焦点. 若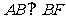 ,则该椭圆的离心率为
,则该椭圆的离心率为
(A)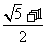 (B)
(B)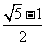
(C)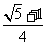 (D)
(D)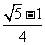
(8)已知函数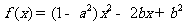 (
(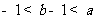 ). 用
). 用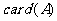 表示集合
表示集合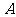 中元素的个数,若使得
中元素的个数,若使得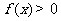 成立的充分必要条件是
成立的充分必要条件是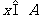 ,且
,且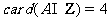 ,则实数
,则实数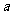 的取值范围是
的取值范围是
(A)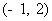 (B)
(B)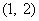
(C)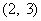 (D)
(D)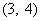
第II卷(非选择题 共110分)
(15)(本题满分13分)
设函数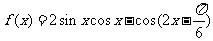 .
.
(Ⅰ)求函数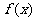 的最小正周期;
的最小正周期;
(Ⅱ)当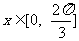 时,求函数
时,求函数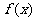 的最大值及取得最大值时的
的最大值及取得最大值时的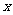 的值.
的值.
(16) (本题满分13分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
|
环数 |
7 |
8 |
9 |
10 |
|
命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为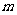 次、
次、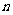 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“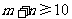 ”的概率.
”的概率.
(17) (本题满分13分)
如图,在四棱锥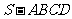 中,底面
中,底面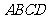 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,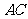 与
与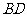 的交点为O.
的交点为O.
(Ⅰ)求证: 平面
平面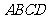 ;
;
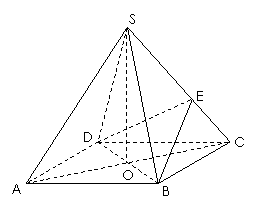 (Ⅱ)已知
(Ⅱ)已知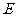 为侧棱
为侧棱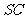 上一个动点. 试问对于
上一个动点. 试问对于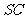 上任意一点
上任意一点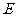 ,平面
,平面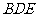 与平面
与平面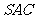 是否垂直?若垂直,请加以证明;若不垂直,请说明理由.
是否垂直?若垂直,请加以证明;若不垂直,请说明理由.
(18) (本题满分14分)
已知函数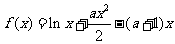 ,
,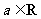 ,且
,且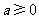 .
.
(Ⅰ)若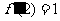 ,求
,求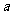 的值;
的值;
(Ⅱ)当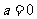 时,求函数
时,求函数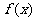 的最大值;
的最大值;
(Ⅲ)求函数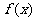 的单调递增区间.
的单调递增区间.
(19) (本题满分13分)
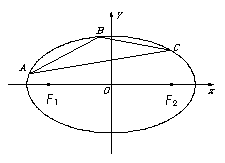 已知椭圆
已知椭圆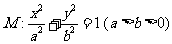 的左右焦点分别为
的左右焦点分别为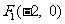 ,
,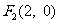 .在椭圆
.在椭圆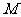 中有一内接三角形
中有一内接三角形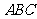 ,其顶点
,其顶点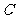 的坐标
的坐标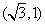 ,
,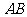 所在直线的斜率为
所在直线的斜率为 .
.
(Ⅰ)求椭圆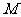 的方程;
的方程;
(Ⅱ)当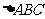 的面积最大时,求直线
的面积最大时,求直线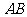 的方程.
的方程.
20.(本题满分14分)
已知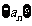 是递增数列,其前
是递增数列,其前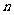 项和为
项和为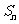 ,
,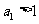 ,且
,且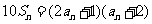 ,
,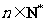 .
.
(Ⅰ)求数列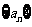 的通项
的通项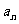 ;
;
(Ⅱ)是否存在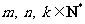 ,使得
,使得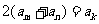 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的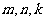 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)设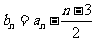 ,若对于任意的
,若对于任意的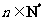 ,不等式
,不等式
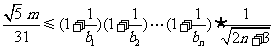 恒成立,求正整数
恒成立,求正整数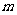 的最大值.
的最大值.
(9)函数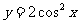 的值域是
.
的值域是
.
 (10)已知向量
(10)已知向量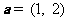 ,
,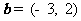 ,如果
,如果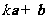 与
与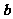 垂直,那么实数
垂直,那么实数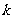 的值为
.
的值为
.
(11)设变量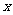 ,
,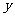 满足
满足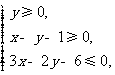
则该不等式组所表示的平面区域的面积等于
;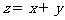 的最大值为
.
的最大值为
.
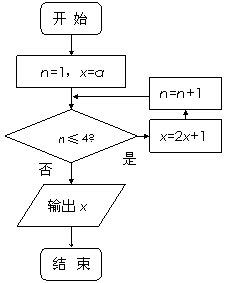
(12)若某程序框图如右图所示,
该程序运行后,输出的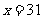 ,
,
则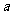 等于
.
等于
.
 (13)上海世博园中的世博轴是一条1000
(13)上海世博园中的世博轴是一条1000 长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为
长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为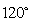 . 据此数据计算,中国馆到世博轴其中一端的距离是
. 据此数据计算,中国馆到世博轴其中一端的距离是
 .
.
(14)已知数列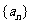 为等差数列,若
为等差数列,若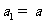 ,
,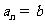 (
(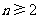 ,
,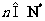 ),则
),则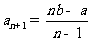 .
.
类比等差数列的上述结论,对等比数列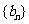 (
(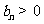 ,
,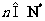 ),若
),若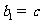 ,
,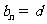
(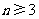 ,
,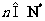 ),则可以得到
),则可以得到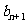 =
.
=
.
(1)已知集合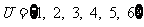 ,集合
,集合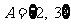 ,集合
,集合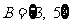 ,则
,则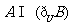
等于
(A)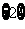 (B)
(B)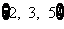 (C)
(C) (D)
(D)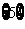
(2)设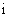 为虚数单位,则复数
为虚数单位,则复数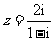 所对应的点位于
所对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(3)过点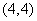 引圆
引圆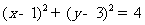 的切线,则切线长是
的切线,则切线长是
(A) 2 (B)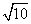 (C)
(C) 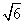 (D)
(D) 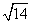
(4)一个正方体的所有顶点都在同一球面上,若球的体积是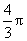 ,则正方体的表面积是
,则正方体的表面积是
(A)8 (B)6 (C)4 (D)3
(5)某校共有学生2000名,各年级男、女学生人数如下表,已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19,现用分层抽样的方法在全校学生中抽取64人,则应在三年级抽取的学生人数为( )
|
|
一年级 |
二年级 |
三年级 |
|
女生 |
385 |
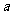 |
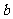 |
|
男生 |
375 |
360 |
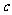 |
(A)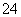 (B)
(B)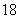 (C)
(C)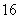 (D)
(D)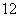
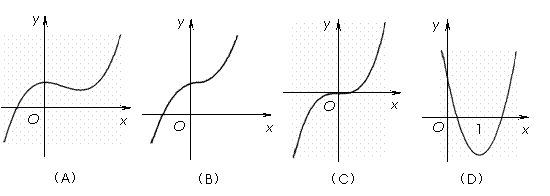 (6)函数
(6)函数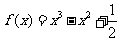 的图象大致是
的图象大致是
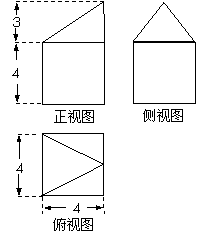
(7)一个几何体的三视图如图所示,则此几何体的体积是
(A)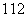 (B)
(B)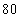
 (C)
(C)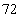 (D)
(D)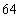
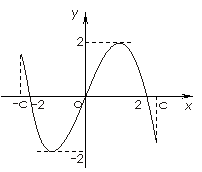
(8)如图所示,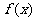 是定义在区间
是定义在区间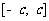 (
(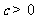 )上的奇函数,令
)上的奇函数,令 ,并有关于函数
,并有关于函数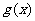 的四个论断:
的四个论断:
①对于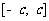 内的任意实数
内的任意实数 (
(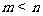 ),
),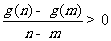 恒成立;
恒成立;
 ②若
②若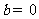 ,则函数
,则函数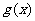 是奇函数;
是奇函数;
③若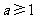 ,
,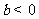 ,则方程
,则方程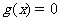 必有3个实数根;
必有3个实数根;
④若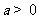 ,则
,则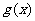 与
与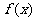 有相同的单调性.
有相同的单调性.
其中正确的是( )
(A)②③ (B)①④
(C)①③ (D)②④
第II卷(非选择题 共110分)
20、(本题满分16分)
已知数列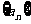 是公差为
是公差为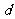
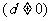 的等差数列,
的等差数列,
数列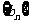 是公比为
是公比为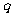 的(q∈R)的等比数列,若函数
的(q∈R)的等比数列,若函数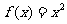 ,且
,且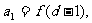
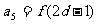 ,
,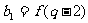 ,
,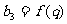 ,
,
(1)求数列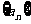 和
和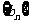 的通项公式;
的通项公式;
(2)设数列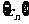 的前n项和为
的前n项和为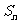 ,对一切
,对一切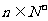 ,都有
,都有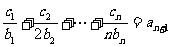 成立,求
成立,求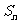
江苏省南通中学2009-2010学年第二学期
19、(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知函数 (其中
(其中 且
且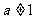 ,
,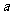 为实数常数).
为实数常数).
(1)若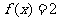 ,求
,求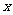 的值(用
的值(用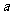 表示);
表示);
(2)若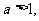 且
且 对于
对于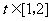 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用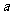 表示).
表示).
18、(本题满分15分)
由于卫生的要求游泳池要经常换水(进一些干净的水同时放掉一些脏水), 游泳池的水深经常变化,已知泰州某浴场的水深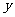 (米)是时间
(米)是时间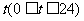 ,(单位小时)的函数,记作
,(单位小时)的函数,记作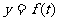 ,下表是某日各时的水深数据
,下表是某日各时的水深数据
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
2 5 |
2 0 |
15 |
20 |
249 |
2 |
151 |
199 |
2 5 |
经长期观测的曲线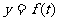 可近似地看成函数
可近似地看成函数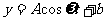
(Ⅰ)根据以上数据,求出函数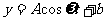 的最小正周期T,振幅A及函数表达式;
的最小正周期T,振幅A及函数表达式;
(Ⅱ)依据规定,当水深大于2米时才对游泳爱好者开放,请依据(1)的结论,判断一天内的上午8 00至晚上20 00之间,有多少时间可供游泳爱好者进行运动
17、(本题满分15分)
已知动点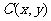 到点
到点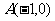 的距离是它到点
的距离是它到点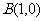 的距离的
的距离的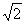 倍.
倍.
(Ⅰ) 试求点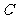 的轨迹方程;
的轨迹方程;
(Ⅱ) 试用你探究到的结果求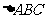 面积的最大值.
面积的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com