
2.已知虚数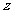 满足
满足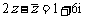 ,则
,则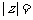 ▲ .
▲ .
1.集合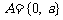 ,集合
,集合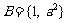 ,若
,若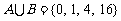 ,则
,则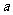 的值为
▲ .
的值为
▲ .
22.(本小题满分12分)
椭圆C的中心在坐标原点O,焦点在y轴上,焦点到相应准线的距离及离心率均为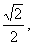 斜率为k的直线l与y轴相交于点P(0,m),与椭圆C相交于相异两点A、B,且
斜率为k的直线l与y轴相交于点P(0,m),与椭圆C相交于相异两点A、B,且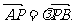
(Ⅰ)求椭圆C的方程;
(Ⅱ)若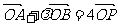 ,求m的取值范围.
,求m的取值范围.
21.(本小题满分12分)
设函数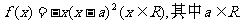
(Ⅰ)当a≠0时,求函数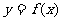 的极值;
的极值;
(Ⅱ)当a>3时,是否存在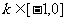 ,使得不等式
,使得不等式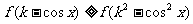 对
对
任意的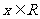 恒成立,若存在,求出k的值,若不存在,说明理由.
恒成立,若存在,求出k的值,若不存在,说明理由.
20.(本小题满分12分)
某商场经销商品,顾客可采用一次性付款或分期付款购买,经销一件该商品,若是一次性收款可获利润300元,若是分期收款可获利润360元。据统计,顾客采用一次性付款的概率为0.6.
(Ⅰ)求3位购买该商品者中至少有一位采用一次性付款的概率;
(Ⅱ)求3位购买者每人购买一件该商品,商场获利润不超过1000元的概率.
19.(本小题满分12分)
已知首项不为零的数列{an}的前n项和为Sn,若对任意的r、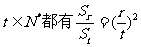
(Ⅰ)判断数列{an}是否为等差数列,并证明你的结论;
(Ⅱ)若a1=1,b1=3,数列{bn}的第n项bn是数列{an}的第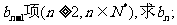
(Ⅲ)在(Ⅱ)的条件下,求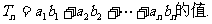
17.(本小题满分10分)
已知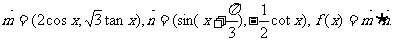
(Ⅰ)求f(x)的最小正周期T;
(Ⅱ)若△ABC的三边a,b,c满足b2=ac,且边b所对的角为B,试求cosB的取值范围,并确定此时f(B)的最大值.
 18.(本小题满分12分)
18.(本小题满分12分)
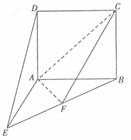
如图:AE⊥平面ABCD,ABCD为正方形,AE=AB,
F为BE的中点.
(Ⅰ)求证:DE//平面ACF;
(Ⅱ)求二面角B-AC-F的余弦值.
16.已知函数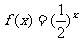 的图象与函数g(x)的图象关于直线y=x对称,令
的图象与函数g(x)的图象关于直线y=x对称,令
h(x)=g(1-|x|),则关于函数h(x)有下列命题:
①h(x)的图象关于原点对称 ②h(x)为偶数
③h(x)的最小值为0 ④h(x)在(0,1)上为减函数
其中正确命题的序号为 (注:将所有正确命题的序号都填上).
15.若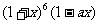 的展开中含x3项的系数是5,则a的值为
.
的展开中含x3项的系数是5,则a的值为
.
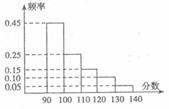 13.某市高三数学抽样考试中,对90分以上
13.某市高三数学抽样考试中,对90分以上
(含90分)的成绩进行统计,其频率分
布图如图所示,若130~140分数段的人数
为90人,则90~100分数段的人数为 .
14.实系数方程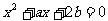 的一根在
的一根在
(0,1)内,另一个根在(1,2)内,
则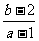 的值域为
.
的值域为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com