
6.若乙地为北京,则丙地的正午太阳高度可能是
A.23°26′ B.66° C.72° D.90°
植物对某地气候的反应称为物候现象。据此回答:
5.丁地的日落时刻是
A.6时 B.15时 C.18时 D.21时
4.四个地点中,纬度数值相同的地点是
A.甲、丁 B.甲、乙、丙
C.丙、丁 D.没有纬度相同的地点
3.图示状态时,下列地理现象中可信的是
A.地表夜晚可能观察到P、Q两星,且都特别亮
B.地表夜晚可能观察到P星,但不易看到Q星
C.北半球各地昼长均可能达到最小值
D.到北冰洋进行科学考察的黄金季节
下图为同一日期甲、乙、丙、丁四个地点的昼长状况,据此回答5-6题。
2.在甲、乙两区域中可能发生的是
A.ABCD四处的水都汇入水域M B.EFG的海拔在750米以上,800米以下
C.在E点可以观察到车站N D.铁路沿线要预防滑坡和泥石流
读右图,P、Q是与地球相邻的大行星,M是地球的自然卫星。分析判断:
1.图甲N处陡崖的最大高度可能是
A.199米 B.549米 C.599米 D.649米
⒖(12分)已知函数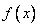 在定义域
在定义域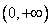 上为增函数,且满足
上为增函数,且满足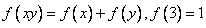 .
.
(1)求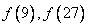 的值;
(2)解不等式:
的值;
(2)解不等式: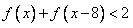 .
.
⒗(12分)已知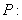 函数
函数 在
在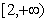 单调递增,
单调递增,
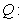 关于
关于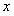 的不等式
的不等式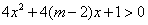
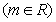 的解集为
的解集为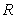 ,
,
若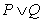 为真命题,
为真命题,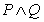 为假命题,求
为假命题,求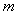 的取值范围.
的取值范围.
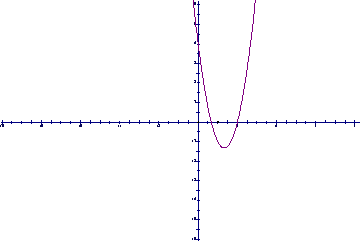
⒘(14分)设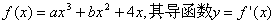 的
的
图象经过点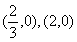 ,如右图所示。
,如右图所示。
⑴求函数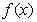 的解析式和极值;
的解析式和极值;
⑵对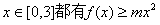 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
⒙(14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的。某市用水收费方法是:水费=基本费+超额费+损耗费。该市规定:
①若每月用水量不超过最低限量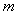 立方米时,只付基本费9元和每户每月的定额损耗费
立方米时,只付基本费9元和每户每月的定额损耗费 元;
元;
②若每月用水量超过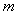 立方米时,除了付基本费和损耗费外,超过部分每立方米付
立方米时,除了付基本费和损耗费外,超过部分每立方米付
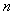 元的超额费;
元的超额费;
③每户每月的损耗费 不超过5元。
不超过5元。
⑴求每户每月水费 (元)和用水量
(元)和用水量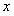 (立方米)的函数关系式;
(立方米)的函数关系式;
⑵该市一家庭去年第一季度的用水量和支付的费用如下表所示:
|
月份 |
用水量(立方米) |
水费(元) |
|
一月份 |
4 |
17 |
|
二月份 |
5 |
23 |
|
三月份 |
2.5 |
11 |
试分析一、二、三各月份的用水量是否超过最低限量,并求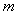 、
、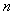 、
、 的值。
的值。
⒚(14分)已知函数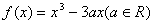 .
.
⑴当 时,求过点
时,求过点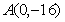 且与函数
且与函数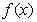 的图象相切的直线
的图象相切的直线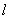 的方程;
的方程;
⑵设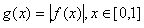 ,求
,求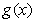 的最大值
的最大值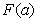 的解析式.
的解析式.
⒛(14分)已知函数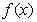 为奇函数,当
为奇函数,当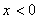 时,
时,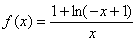 .
.
⑴求当 时,
时,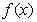 的表达式;
的表达式;
⑵对于任意 ,比较
,比较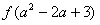 与
与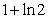 的大小,证明你的结论;
的大小,证明你的结论;
⑶若对任意的 及
及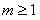 ,不等式
,不等式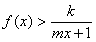 恒成立,求正整数
恒成立,求正整数 的最大值。
的最大值。
广东省汕头市金山中学
20.(本小题满分14分)已知偶函数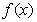 对任意的
对任意的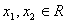 ,恒有
,恒有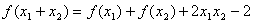 ,
,
(1)求 的值及
的值及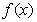 的表达式;
的表达式;
(2)设函数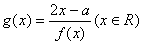 ,若函数
,若函数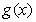 在区间
在区间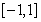 上是增函数,求实数
上是增函数,求实数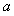 的值组成的集合A;
的值组成的集合A;
(3)在(2)的条件下,设关于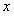 的方程
的方程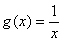 的两个非零实根为
的两个非零实根为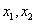 ,试问:是否存在实数m,使得不等式
,试问:是否存在实数m,使得不等式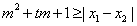 对
对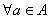 及
及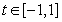 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。
广东省汕头市金山中学10届高三上期期中考试
19.(本小题满分14分)设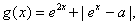
 ,其中
,其中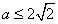 ,
,
(1)当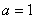 时,函数
时,函数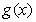 是否存在零点,若存在,求出所有零点;若不存在,说明理由。
是否存在零点,若存在,求出所有零点;若不存在,说明理由。
(2)求函数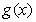 的最小值。
的最小值。
18.(本小题满分14分)已知函数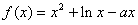 (
(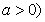
(1)若函数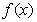 在
在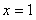 处取得极值,求
处取得极值,求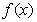 。
。
(2)求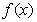 的单调区间;
的单调区间;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com