
22. (本小题满分14分)数列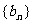 满足
满足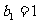 ,
,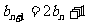 ,若数列
,若数列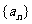 满足
满足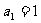 ,
,
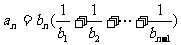
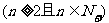
(1)求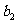 ,
,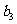 ,
,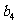 及
及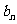 ;
;
(2)证明: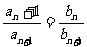
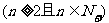 ;
;
(3)求证: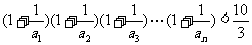 .
.
21.(本小题满分12)已知椭圆C: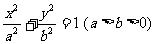 ,经过点
,经过点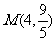 ,过点M向x轴作垂线恰经过椭圆C的焦点,
,过点M向x轴作垂线恰经过椭圆C的焦点,
(1)求椭圆方程;
(2)设直线l与椭圆C相交于A,B两点,且满足|AF|,|MF|,|BF|成等差数列.若AB的垂直平分线交x轴于点T,求直线MT的斜率.
20.(本小题满分12)己知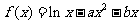 .
.
(Ⅰ)若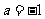 ,函数
,函数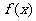 在其定义域内是增函数,求
在其定义域内是增函数,求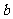 的取值范围;
的取值范围;
(Ⅱ)当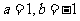 时,证明函数
时,证明函数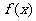 只有一个零点;
只有一个零点;
19.(本小题满分12分)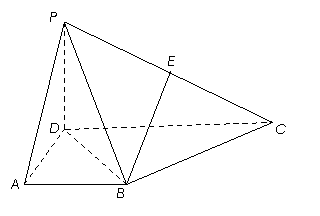 在四棱锥
在四棱锥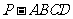 中,侧面
中,侧面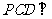 底面
底面 ,
,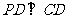 ,为
,为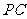 中点,底面
中点,底面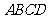 是直角梯形,
是直角梯形,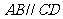 ,
,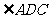 =90°,
=90°,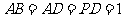 ,
,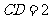 .(1)求证:
.(1)求证: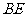
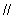 平面
平面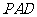 ;
;
(2)求证: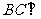 平面
平面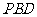 ;
;
(3)设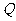 为侧棱
为侧棱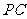 上一点,
上一点,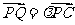 ,
,
试确定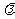 的值,使得二面角
的值,使得二面角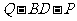 为45°.
为45°.
18.(本小题满分12分)某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是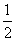 .同样也假定D受A、B和C感染的概率都是
.同样也假定D受A、B和C感染的概率都是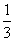 .在这种假定之下,B、C、D中直接受A感染的人数
.在这种假定之下,B、C、D中直接受A感染的人数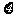 就是一个随机变量.写出
就是一个随机变量.写出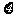 的分布列(不要求写出计算过程),并求
的分布列(不要求写出计算过程),并求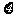 的均值(即数学期望)
的均值(即数学期望)
17.(本小题满分12分)已知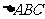 中,、
中,、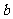 、是三个内角、、
、是三个内角、、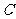 的对边,关于的不等式
的对边,关于的不等式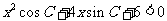 的解集是空集.
的解集是空集.
(1)求角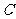 的最大值;
的最大值;
(2)若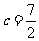 ,
,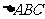 的面积
的面积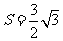 ,求当角
,求当角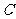 取最大值时
取最大值时 的值.
的值.
16.设函数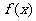 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数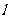 使得对于任意
使得对于任意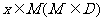 ,有
,有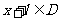 ,且
,且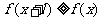 ,则称
,则称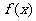 为M上的
为M上的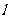 高调函数。如果定义域为
高调函数。如果定义域为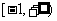 的函数
的函数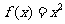 为
为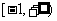 上的高调函数,那么实数的取值范围是
。如果定义域为R的函数
上的高调函数,那么实数的取值范围是
。如果定义域为R的函数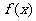 是奇函数,当
是奇函数,当 时,
时,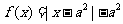 ,且
,且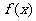 为R上的4高调函数,那么实数的取值范围是 。
为R上的4高调函数,那么实数的取值范围是 。
15. 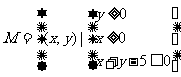 ,
, 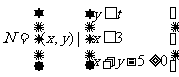 ,
,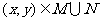 ,当
,当
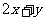 取得最大值时,
取得最大值时,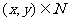 ,
,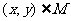 ,则实数的取值范围是
。
,则实数的取值范围是
。
14.已知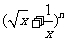
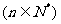 展开式中常数项是
展开式中常数项是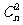 ,则的值为 。
,则的值为 。
13.已知向量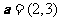 ,
,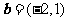 ,则在
,则在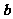 方向上的投影等于
.
方向上的投影等于
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com