
1.下列过程中,不直接依赖细胞膜的流动性就能完成的是
A.植物体细胞杂交中原生质体融合 B.mRNA与游离核糖体的结合
C.胰岛B细胞分泌胰岛素 D.吞噬细胞对抗原的摄取
21.已知偶函数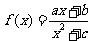 (
(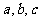 是常数)的导函数为
是常数)的导函数为 且
且
 数列
数列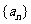 满足
满足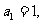 且当
且当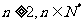 时,
时,
(1)求函数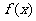 的解析式;
的解析式;
(2)求证: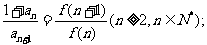
(3)求证:
20.如图,在椭圆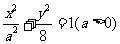 中,
中,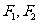 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点, 分别为椭圆的左、右顶点,
分别为椭圆的左、右顶点,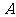 为椭圆在第一象限内的任意一点,直线
为椭圆在第一象限内的任意一点,直线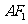 交椭圆于另一点
交椭圆于另一点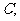 交
交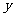 轴于点
轴于点 且点
且点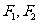 三等分线段
三等分线段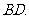
(1)求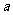 的值;
的值;
 (2)若四边形
(2)若四边形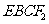 为平行四边形,求点
为平行四边形,求点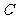 的坐标;
的坐标;
(3)当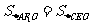 时,求直线
时,求直线 的方程.
的方程.
19.已知
(1)如果函数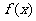 的单调递减区间为
的单调递减区间为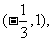 求函数
求函数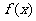 的解析式;
的解析式;
(2)(理)若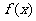 的导函数为
的导函数为 对任意
对任意 不等式
不等式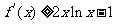 恒成立,求实数
恒成立,求实数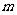 的取值范围.
的取值范围.
(文)若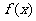 的导函数为
的导函数为 对任意
对任意 不等式
不等式 恒成立,求实数
恒成立,求实数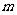 的取值范围.
的取值范围.
18.如图,在四棱柱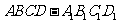 中,
中,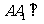 底面
底面 底面
底面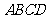 是菱形,
是菱形,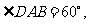
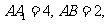 点
点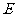 在棱
在棱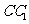 上,点
上,点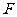 是棱
是棱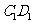 的中点.
的中点.
(1)若点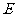 是棱
是棱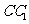 的中点,求证:
的中点,求证: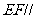 平面
平面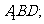
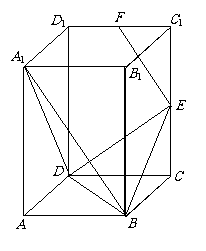 (2)试确定点
(2)试确定点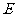 的位置,使得
的位置,使得 为直二面角,并说明理由.
为直二面角,并说明理由.
17.甲、乙两人共同抛掷一枚硬币,规定硬币正面朝上甲得1分,否则乙得1分,先积得3分者获胜,并结束游戏.
(1)求在前3次抛掷中甲得2分,乙得1分的概率;
(2)若甲已经积得2分,乙已经积得1分,求甲最终获胜的概率;
(3)(只理科做)用 表示决出胜负抛硬币的次数,求
表示决出胜负抛硬币的次数,求 的分布列及数学期望.
的分布列及数学期望.
16.在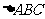 中,角
中,角 所对的边分别为
所对的边分别为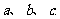
已知向量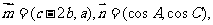 且
且
(1)求角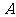 的大小; (2)若
的大小; (2)若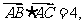 求边
求边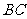 的最小值.
的最小值.
15.若从数字0,1,2,3,4,5中任取三个不同的数作为二次函数 的系数,则与
的系数,则与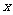 轴有公共点的二次函数的概率是_________________.
轴有公共点的二次函数的概率是_________________.
14.(理)已知函数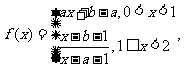 其中
其中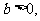 若
若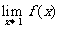 存在,且
存在,且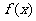 在
在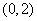 上有最大值,则
上有最大值,则 的取值范围是______________.
的取值范围是______________.
(文)若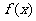 是以5为周期的奇函数,
是以5为周期的奇函数,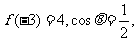 则
则 ________.
________.
13.已知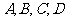 在同一球面上,
在同一球面上,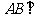 平面
平面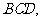
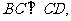 若
若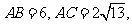
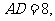
则 的球面距离为____________.
的球面距离为____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com