
2.已知等比数列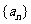 中,
中,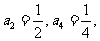 则
则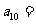 ( )
( )
A.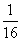 B.
B.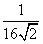 C.
C. D.
D.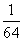
1.(理)若复数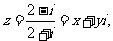
 则
则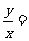 ( )
( )
A.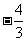 B.
B. C.
C.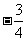 D.
D.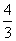
(文)设集合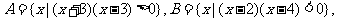 则
则 ( )
( )
A.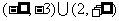 B.
B.
C.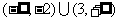 D.
D.
20. (湖南师大附中2010届高三第五次月考) 已知数列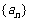 的前
的前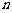 项和
项和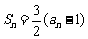 ,
,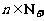 .
.
(Ⅰ)求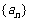 的通项公式;
的通项公式;
(Ⅱ)设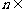 N+,集合
N+,集合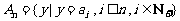 ,
,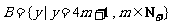 .现在集合
.现在集合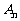 中随机取一个元素
中随机取一个元素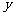 ,记
,记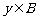 的概率为
的概率为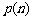 ,求
,求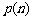 的表达式.
的表达式.
19. 在平面直角坐标系xOy中,已知三点A(-1,0),B(1,0),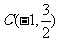 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C.
(I)求椭圆的方程;

 w_w w. k#s5_
w_w w. k#s5_
(II)设点D(0,1),是否存在不平行于x轴的直线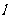 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使
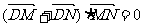 ?若存在,求出直线
?若存在,求出直线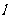 斜率的取值范围;若不存在,请说明理由:@w@w.k@
斜率的取值范围;若不存在,请说明理由:@w@w.k@
(III)对于y轴上的点P(0,n)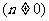 ,存在不平行于x轴的直线
,存在不平行于x轴的直线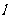 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使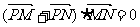 ,试求实数n的取值范围.#s5_
,试求实数n的取值范围.#s5_
18. (山东省临沂高三数学(理工)教学质量监测) 已知函数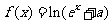 (
(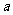 为常数)是R上的奇函数,函数g(x)=
为常数)是R上的奇函数,函数g(x)=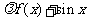 是区间
是区间 上的减函数.
上的减函数.
(Ⅰ)求 的值;
的值;
(Ⅱ)若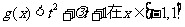 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程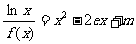 的根的个数.
的根的个数.
17.某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
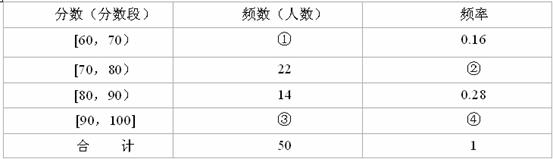
(Ⅰ)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(Ⅱ)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖.如果前三道题都答错,就不再答第四题.某同学进入决赛,每道题答对的概率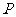 的值恰好与频率分布表中不少于80分的频率的值相同.
的值恰好与频率分布表中不少于80分的频率的值相同.
①求该同学恰好答满4道题而获得一等奖的概率;
②记该同学决赛中答题个数为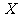 ,求
,求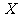 的分布列及数学期望.
的分布列及数学期望.
08福建15.已知向量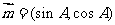 ,
,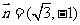 ,
,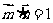 ,且
,且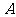 为锐角.
为锐角.
(Ⅰ)求角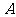 的大小;
的大小;
(Ⅱ)求函数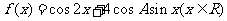 的值域.
的值域.
16. 如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4. (Ⅰ)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
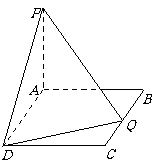 (Ⅱ)当边BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值.
(Ⅱ)当边BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值.
14.若函数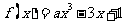 对于
对于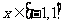 总有
总有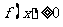 成立,则
成立,则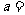 _____.
_____.
13.设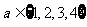 ,
, ,则函数
,则函数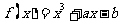 在区间
在区间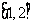 上
上
有零点的概率为_____________.
12.程序框图(即算法流程图)如图所示,其输出结果是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com