
17.(理)某射手向一个气球射击,若各次射击相互独立,且每次射击击破气球的概率均为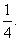
(1)若该射手共射击三次,求第三次射击才将球击破的概率;
(2)给出两种积分方案。方案甲:提供三次射击机会和一张700点的积分卡,若未击中的次数为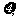
则扣除积分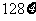 点;方案乙:提供四次射击机会和一张1000点的积分卡,若未击中的次数为
点;方案乙:提供四次射击机会和一张1000点的积分卡,若未击中的次数为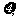
则扣除积分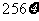 点。在执行上述两种方案时规定:若将球击破,则射击停止;若未击破,则继续射击直至用完规定的射击次数。问:该射手应选择哪种方案才能使积分卡剩余点数最多,并说明理由.
点。在执行上述两种方案时规定:若将球击破,则射击停止;若未击破,则继续射击直至用完规定的射击次数。问:该射手应选择哪种方案才能使积分卡剩余点数最多,并说明理由.
(文)袋中有分别写着“团团”和“圆圆”的两种玩具共7个,且形状完全相同,从中任取2个玩具都是“圆圆”的概率为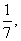 A、B两人不放回地从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,…直到两人中有一人取到“圆圆”时即停止游戏,每个玩具在每一次被取出的机会是均等的,用
A、B两人不放回地从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,…直到两人中有一人取到“圆圆”时即停止游戏,每个玩具在每一次被取出的机会是均等的,用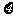 表示游戏终止时取玩具的次数.
表示游戏终止时取玩具的次数.
(1)求袋中“圆圆”的个数; (2)求 的概率.
的概率.
16.在 中,
中, 分别为角
分别为角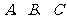 所对的边,且
所对的边,且
(1)求角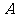 的大小;(2)若
的大小;(2)若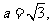 设
设 的周长为
的周长为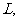 求
求 的最大值.
的最大值.
15.抛物线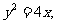 焦点为
焦点为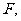
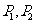 在其准线上,若抛物线上有两点
在其准线上,若抛物线上有两点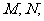 使得
使得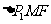 是以
是以 为斜边的等腰直角三角形且
为斜边的等腰直角三角形且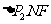 为正三角形,则
为正三角形,则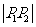 的最小值是_____________.
的最小值是_____________.
14.9名志愿者, 为教师,
为教师,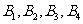 为医生,
为医生, 为学生. 现从中选出教师1名、医生2名、学生1名,则
为学生. 现从中选出教师1名、医生2名、学生1名,则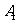 被选中且
被选中且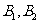 最多有1名被选中的概率为____________.
最多有1名被选中的概率为____________.
13.若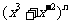 的展开式中只有第5项的系数最大,则展开式中
的展开式中只有第5项的系数最大,则展开式中 项的系数为______________.
项的系数为______________.
12.直线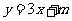 和圆
和圆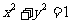 交于
交于 两点,以
两点,以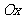 为始边,
为始边, 为终边的角分别为
为终边的角分别为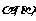 则
则 _________.
_________.
11.(理)随机变量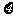 服从正态分布
服从正态分布 若
若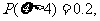 则
则 __________.
__________.
(文)今年“3.15”某报社做了一次关于“手机垃圾短信”的调查,在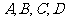 四个单位回收的问卷数依次成等差数列,共回收了2000份,因报道需要,再从回收的问卷中按单位分层抽取容量为300的样本. 若在
四个单位回收的问卷数依次成等差数列,共回收了2000份,因报道需要,再从回收的问卷中按单位分层抽取容量为300的样本. 若在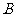 单位抽取60份,则在
单位抽取60份,则在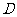 单位抽取________份.
单位抽取________份.
10.已知定直线 与平面
与平面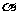 成45°角,点
成45°角,点 是平面
是平面 内的一个动点,且点
内的一个动点,且点 到直线
到直线 的距离为2,
的距离为2,
则动点 的轨迹的离心率是( )
的轨迹的离心率是( )
A. B.
B. C.
C.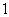 D.
D.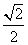
9.约束条件: 当
当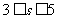 时,函数
时,函数 的最大值的变化范围是( )
的最大值的变化范围是( )
A.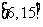 B.
B.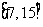 C.
C.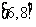 D.
D.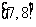
8. 5人争夺一次比赛的前三名,组织者对前三名发给不同的奖品,若
5人争夺一次比赛的前三名,组织者对前三名发给不同的奖品,若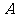 获奖,
获奖,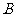
不是第一名,则不同的发奖方式共有( )
A.30种 B.72种 C.24种 D.14种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com