
20.(满分19分)本题有3小题,第1小题5分,第2小题5分,第3小题9分.
已知定义在 上的函数
上的函数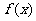 和数列
和数列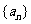 满足下列条件:
满足下列条件:
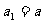 ,
,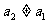 ,当
,当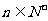 且
且 时,
时,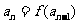 且
且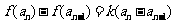 .
.
其中 、
、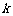 均为非零常数.
均为非零常数.
(1)若数列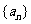 是等差数列,求
是等差数列,求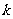 的值;
的值;
(2)令
 ,若
,若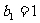 ,求数列
,求数列 的通项公式;
的通项公式;
(3)证明:数列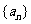 为等比数列的充要条件是
为等比数列的充要条件是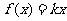
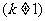 .
.
19.(满分16分)本题有2小题,第1小题6分,第2小题10分.
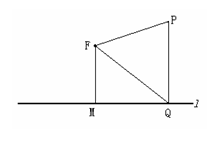 如图,平面上定点
如图,平面上定点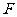 到定直线
到定直线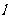 的距离
的距离 ,
,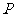 为该平面上的动点,过
为该平面上的动点,过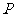 作直线
作直线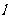 的垂线,垂足为
的垂线,垂足为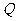 ,且
,且 .
.
(1)试建立适当的平面直角坐标系,求动点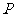 的轨迹
的轨迹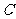 的方程;
的方程;
(2)过点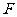 的直线交轨迹
的直线交轨迹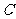 于
于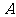 、
、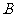 两点,交直线
两点,交直线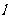 于点
于点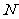 ,
,
已知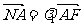 ,
,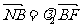 ,求证:
,求证: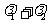 为定值.
为定值.
18.(满分14分)本题有2小题,第1小题6分,第2小题8分.
某企业去年年底给全部的800名员工共发放2000万元年终奖,该企业计划从今年起,10年内每年发放的年终奖都比上一年增加60万元,企业员工每年净增 人.
人.
(1)若 ,在计划时间内,该企业的人均年终奖是否会超过3万元?
,在计划时间内,该企业的人均年终奖是否会超过3万元?
(2)为使人均年终奖年年有增长,该企业每年员工的净增量不能超过多少人?
17. (满分14分)本题有2小题,第1小题7分,第2小题7分.
(满分14分)本题有2小题,第1小题7分,第2小题7分.
如图,在平行六面体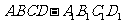 中,
中,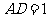 ,
,
 ,
,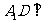 平面
平面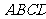 ,
,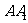 与底面
与底面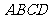 所成角
所成角
为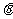 ,
,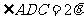 .
.
(1)若 ,求异面直线
,求异面直线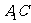 与
与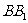 所成角的大小;
所成角的大小;
(2)求平行六面体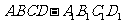 的体积
的体积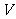 的取值范围.
的取值范围.
应的题号)内写出必要的步骤.
16.(满分12分)本题有2小题,第1小题5分,第2小题7分.
设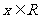 ,
,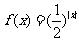 .
.
(1)请在所给的平面直角坐标系中画出函数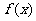 的大致图像;
的大致图像;
(2)若不等式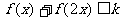 对于任意的
对于任意的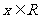 恒成立,求实数
恒成立,求实数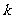 的取值范围.
的取值范围.
15.已知方程 的根大于
的根大于 ,则实数
,则实数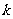 满足[ ]
满足[ ]
A.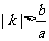 B.
B. C.
C.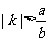 D.
D.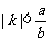
14.将正三棱柱截去三个角(如图1所示A、B、C分别是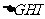 三边的中点)得到的几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为
[ ]
三边的中点)得到的几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为
[ ]


13.若 ,则
,则 [ ]
[ ]
A.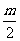 B.
B.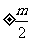 C.
C.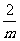 D.
D.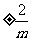
12.设函数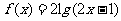 ,则
,则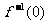 的值为
[ ]
的值为
[ ]
A.0 B.1 C.10 D.不存在
11.设双曲线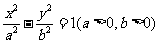 的半焦距为
的半焦距为 .已知原点到直线
.已知原点到直线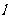 :
: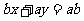 的距离等于
的距离等于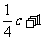 ,则
,则 的最小值为_________.
的最小值为_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com