
3.已知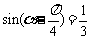 ,则
,则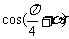 的值等于 ( )
的值等于 ( )
A.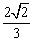 B.-
B.-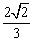 C.
C.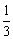 D.-
D.-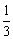
2. 某林场有树苗30000棵,其中松树苗4000棵,为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为 ( )
A.25 B.30 C.15 D.20
1.设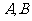 是非空集合,定义
是非空集合,定义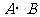 ={
={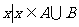 且
且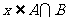 },己知
},己知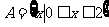
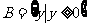 ,则
,则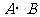 等于 ( )
等于 ( )
A.(2,+∞) B.[0,1]∪[2,+∞]
C.[0,1]∪(2,+∞) D.[0,1]∪(2,+∞)
22.本小题满分12分)已知等比数列{an}中,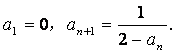
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明: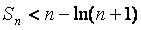 ;
;
(Ⅲ)设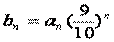 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有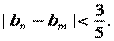
21.(本小题满分12分)已知椭圆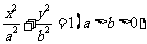 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线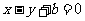 是抛物线
是抛物线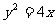 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点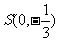 的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ?
若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ?
若存在,求点T坐标;若不存在,说明理由.
20.(本小题满分12分)已知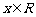 ,函数
,函数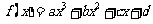 在
在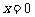 处取得极值,曲线
处取得极值,曲线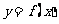 过原点
过原点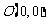 和点
和点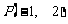 .若曲线
.若曲线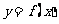 在点
在点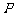 处的切线
处的切线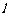 与直线
与直线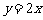 的夹角为
的夹角为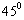 ,且直线
,且直线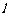 的倾斜角
的倾斜角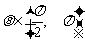
(Ⅰ)求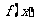 的解析式;
的解析式;
(Ⅱ)若函数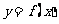 在区间
在区间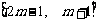 上是增函数,求实数
上是增函数,求实数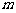 的取值范围;
的取值范围;
(Ⅲ)若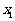 、
、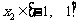 ,求证:
,求证: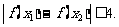
19.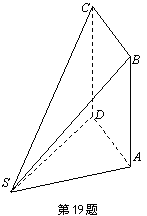 (本题满分12分)如图,多面体ABCDS中,面ABCD为矩形,
(本题满分12分)如图,多面体ABCDS中,面ABCD为矩形,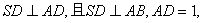
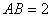 ,
,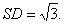
(I)求证:CD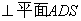 ;
;
(II)求AD与SB所成角的余弦值;
(III)求二面角A-SB-D的余弦值.
18.(本题满分12分)国庆前夕,我国具有自主知识产权的“人甲型H1N1流感病毒核酸检测试剂盒”(简称试剂盒)在上海进行批量生产,这种“试剂盒”不仅成本低操作简单,而且可以准确诊断出“甲流感”病情,为甲型H1N1流感疫情的防控再添一道安全屏障.某医院在得到“试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为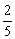 .
.
(I)求出这5位发热病人中“甲流感”患者的人数;
(II)若用“试剂盒”逐个检测这5位发热病人,直到能确定“甲流感”患者为止,设ξ表示检测次数,求ξ的分布列及数学期望Eξ.
17.(本题满分10分)已知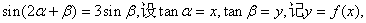
(Ⅰ)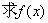 的解析表达式;
的解析表达式;
(Ⅱ)若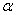 角是一个三角形的最小内角,试求函数
角是一个三角形的最小内角,试求函数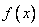 的值域.
的值域.
16.给出下列命题:
A.函数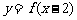 和
和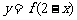 的图象关于直线
的图象关于直线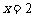 对称.
对称.
B.已知函数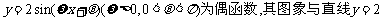 的交点的横坐标为
的交点的横坐标为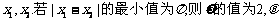 的值为
的值为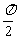 .
.
C.底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
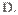 若
若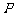 为双曲线
为双曲线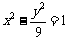 上的一点,
上的一点,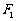 、
、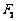 分别为双曲线的左右焦点,且
分别为双曲线的左右焦点,且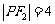 ,则
,则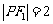 或
或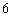 .
.
其中k_s_5_u正确的命题是 (把所有k_s_5_u正确的命题的选项都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com