
23.(本小题满分8分)已知数列{an}的前n项和为Sn,an=5Sn-3(n∈N),求证:数列{an}是等比数列。
24 (本小题满分8分)设
(本小题满分8分)设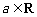 ,
,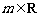 ,函数
,函数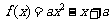 。若
。若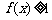 对
对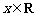 都成立,求
都成立,求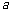 的取值范围。
的取值范围。
25 (本小题满分8分)如图,△ABC是等腰直角三角形, AC=BC=a,P是△ABC所在平面外一点,
(本小题满分8分)如图,△ABC是等腰直角三角形, AC=BC=a,P是△ABC所在平面外一点,
PA=PB=PC=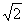 a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.
a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.

21.(本小题满分8分)已知函数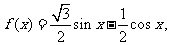 x
x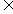 R
R 求
求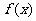 的最大值,并求使
的最大值,并求使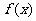 取得最大值时x的集合
取得最大值时x的集合 22.(本小题满分8分)若经过两点A(
22.(本小题满分8分)若经过两点A(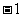 , 0),B(0, 2)的直
, 0),B(0, 2)的直
线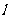 与圆
与圆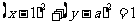 相切,求
相切,求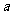 的值
的值
20.已知在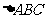 中,
中,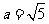 ,
,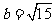 ,
,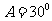 ,则
,则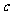 等于
等于 
一、选择题答题卡:班级:_______姓名:___________考号:_______
16.正方体的棱长为1,它的顶点都在同一个球面上,那么这个球的表面积为 
17 若直线
若直线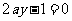 与直线
与直线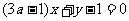 平行,则实数
平行,则实数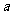 等于
等于 
18 已知等边三角形ABC的边长为1,则
已知等边三角形ABC的边长为1,则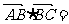
19 已知x>0,那么3x+≥____________
已知x>0,那么3x+≥____________
1 函数
函数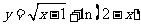 的定义域是( )(A)
的定义域是( )(A) (B)
(B)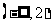 (C)
(C)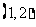 (D)
(D)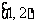
2 某中学有高级教师28人,中级教师54人,初级教师81人,为了调查他们的身体状况,从他们中抽取容量为36的样本,最适合抽取样本的方法是( )
某中学有高级教师28人,中级教师54人,初级教师81人,为了调查他们的身体状况,从他们中抽取容量为36的样本,最适合抽取样本的方法是( )
A.简单随机抽样 B.系统抽样C.分层抽样 D.先从高级教师中随机剔除1人,再用分层抽样
3 函数
函数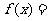
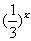 在区间
在区间 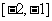 上的最大值是( )A.1 B.9 C. 27 D.
上的最大值是( )A.1 B.9 C. 27 D.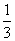
4 在编制将两变量a,b的数值交换的正确的程序中,必须使用到的语句是( )
在编制将两变量a,b的数值交换的正确的程序中,必须使用到的语句是( )
A.输入、输出语句B. 输入、输出语句,条件语句
C.输入、输出语句,赋值语句D. 输入、输出语句,循环语句
5 不等式
不等式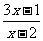
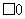 的解集为( )
的解集为( )
(A){x|
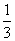 ≤x≤2}(B){x|
≤x≤2}(B){x|
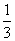 ≤x<2}(C){x|
x>2或x≤
≤x<2}(C){x|
x>2或x≤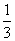 }(D){x|
x<2}
}(D){x|
x<2}
6 已知
已知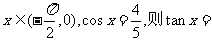 ( )(A)
( )(A)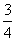 (B)-
(B)-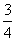 (C)
(C)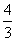 (D)-
(D)-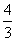
7 在空间中,a、b、c是两两不重合的三条直线,
在空间中,a、b、c是两两不重合的三条直线,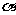 、
、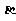 、
、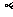 是两两不重合的三个平面,下列命题正确的是( )
是两两不重合的三个平面,下列命题正确的是( )
(A)若两直线a、b分别与平面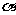 平行,则a//b (B)若直线a与平面
平行,则a//b (B)若直线a与平面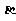 内的一条直线b平行,则
内的一条直线b平行,则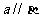
(C)若直线a与平面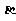 内的两条直线b、c都垂直,则
内的两条直线b、c都垂直,则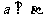
(D)若平面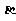 内的一条直线a垂直平面
内的一条直线a垂直平面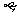 则
则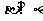
8 若函数
若函数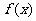 的图象与函数
的图象与函数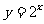 的图象关于直线
的图象关于直线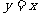 对称,则( )
对称,则( )
(A)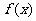
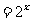 (B)
(B)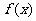
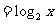 (C)
(C)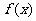
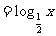 (D)
(D)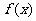
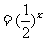
9 过点
过点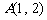 且与直线
且与直线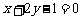 垂直的直线方程是( )
垂直的直线方程是( )
A.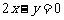 B.
B.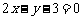 C.
C.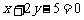 D.
D.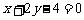
10 已知向量
已知向量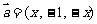 ,向量
,向量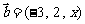 ,若
,若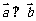 ,则实数
,则实数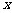 的值是( )
的值是( )
A.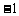 或
或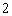 B.
B.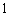 或
或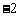 C.
C.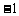 或
或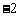 D.
D.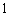 或
或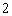
11 在平行四边形ABCD中,若
在平行四边形ABCD中,若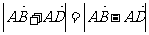 ,则必有( )
,则必有( )
A.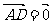 B.
B.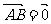 或
或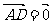 C.ABCD是矩形 D.ABCD是正方形
C.ABCD是矩形 D.ABCD是正方形
 12
12 如图Rt△
如图Rt△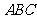 中,
中,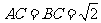 ,
, 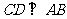 ,沿
,沿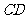 将△
将△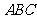 折成
折成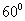 的二面角A-CD-B,则折叠后点
的二面角A-CD-B,则折叠后点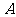 到平面
到平面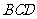 的距离是( )
的距离是( )
(A)1(B)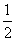 (C)
(C)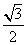 (D)2
(D)2
13 已知数列{an}的前n项和Sn=
已知数列{an}的前n项和Sn=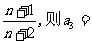 ( )(A)
( )(A)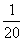 (B)
(B)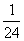 (C)
(C)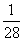 (D)
(D)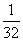
14 若直线
若直线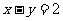 被圆
被圆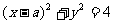 所截得的弦长为
所截得的弦长为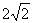 ,则实数a的值为( )
,则实数a的值为( )
(A)–1或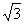 (B)1或3 (C)–2或6 (D)0或4
(B)1或3 (C)–2或6 (D)0或4
15 在
在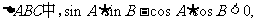 则这个三角形一定是( )
则这个三角形一定是( )
(A)锐角三角形 (B)钝角三角形 (C)直角三角形 (D等腰三角形
23、(本小题满分10分)
已知△ABC的三边长都是有理数。
(1)求证cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数。
[解析] 本题主要考查余弦定理、数学归纳法等基础知识,考查推理论证的能力与分析问题、解决问题的能力。满分10分。
(方法一)(1)证明:设三边长分别为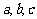 ,
,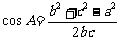 ,∵
,∵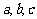 是有理数,
是有理数,
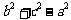 是有理数,分母
是有理数,分母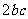 为正有理数,又有理数集对于除法的具有封闭性,
为正有理数,又有理数集对于除法的具有封闭性,
∴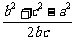 必为有理数,∴cosA是有理数。
必为有理数,∴cosA是有理数。
(2)①当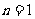 时,显然cosA是有理数;
时,显然cosA是有理数;
当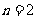 时,∵
时,∵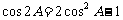 ,因为cosA是有理数, ∴
,因为cosA是有理数, ∴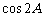 也是有理数;
也是有理数;
②假设当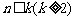 时,结论成立,即coskA、
时,结论成立,即coskA、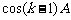 均是有理数。
均是有理数。
当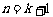 时,
时,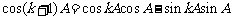 ,
,
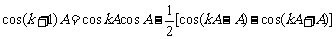 ,
,
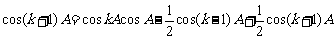 ,
,
解得: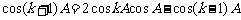
∵cosA,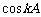 ,
,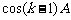 均是有理数,∴
均是有理数,∴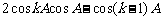 是有理数,
是有理数,
∴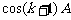 是有理数。
是有理数。
即当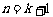 时,结论成立。
时,结论成立。
综上所述,对于任意正整数n,cosnA是有理数。
(方法二)证明:(1)由AB、BC、AC为有理数及余弦定理知
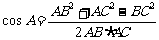 是有理数。
是有理数。
(2)用数学归纳法证明cosnA和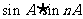 都是有理数。
都是有理数。
①当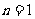 时,由(1)知
时,由(1)知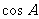 是有理数,从而有
是有理数,从而有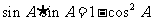 也是有理数。
也是有理数。
②假设当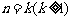 时,
时,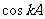 和
和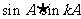 都是有理数。
都是有理数。
当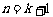 时,由
时,由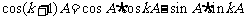 ,
,
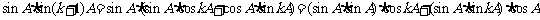 ,
,
及①和归纳假设,知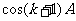 和
和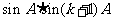 都是有理数。
都是有理数。
即当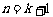 时,结论成立。
时,结论成立。
综合①、②可知,对任意正整数n,cosnA是有理数。
22、(本小题满分10分)
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的利润不少于10万元的概率。
[解析] 本题主要考查概率的有关知识,考查运算求解能力。满分10分。
解:(1)由题设知,X的可能取值为10,5,2,-3,且
P(X=10)=0.8×0.9=0.72, P(X=5)=0.2×0.9=0.18,
P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02。
由此得X的分布列为:
|
X |
10 |
5 |
2 |
-3 |
|
P |
0.72 |
0.18 |
0.08 |
0.02 |
(2)设生产的4件甲产品中一等品有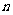 件,则二等品有
件,则二等品有 件。
件。
由题设知 ,解得
,解得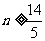 ,
,
又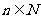 ,得
,得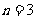 ,或
,或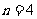 。
。
所求概率为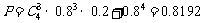
答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
21.[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
A. 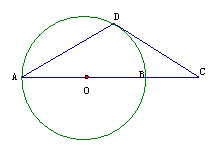 选修4-1:几何证明选讲
选修4-1:几何证明选讲
(本小题满分10分)
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
[解析] 本题主要考查三角形、圆的有关知识,考查推理论证能力。
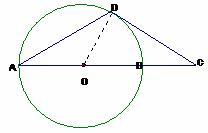 (方法一)证明:连结OD,则:OD⊥DC,
(方法一)证明:连结OD,则:OD⊥DC,
又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=300,∠DOC=600,
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
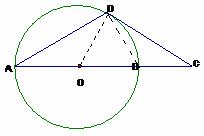 因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC 是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
故AB=2BC。
B. 选修4-2:矩阵与变换
(本小题满分10分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。满分10分。
解:由题设得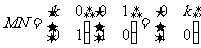
由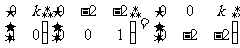 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1(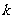 ,-2)。
,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是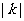 ,则由题设知:
,则由题设知: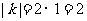 。
。
所以k的值为2或-2。
C. 选修4-4:坐标系与参数方程
(本小题满分10分)
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
[解析] 本题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力。满分10分。
解: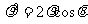 ,圆ρ=2cosθ的普通方程为:
,圆ρ=2cosθ的普通方程为: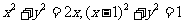 ,
,
直线3ρcosθ+4ρsinθ+a=0的普通方程为: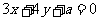 ,
,
又圆与直线相切,所以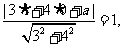 解得:
解得: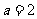 ,或
,或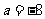 。
。
D.选修4-5:不等式选讲
(本小题满分10分)
设a、b是非负实数,求证: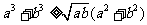 。
。
[解析] 本题主要考查证明不等式的基本方法,考查推理论证的能力。满分10分。
(方法一)证明: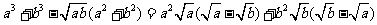
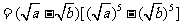
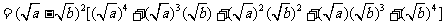
因为实数a、b≥0,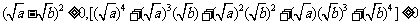
所以上式≥0。即有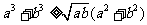 。
。
(方法二)证明:由a、b是非负实数,作差得
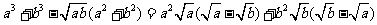
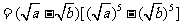
当 时,
时,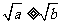 ,从而
,从而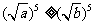 ,得
,得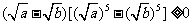 ;
;
当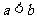 时,
时,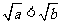 ,从而
,从而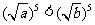 ,得
,得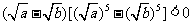 ;
;
所以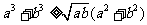 。
。
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
20、(本小题满分16分)
设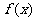 是定义在区间
是定义在区间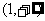 上的函数,其导函数为
上的函数,其导函数为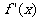 。如果存在实数
。如果存在实数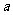 和函数
和函数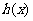 ,其中
,其中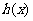 对任意的
对任意的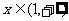 都有
都有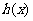 >0,使得
>0,使得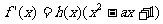 ,则称函数
,则称函数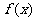 具有性质
具有性质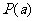 。
。
(1)设函数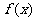
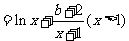 ,其中
,其中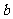 为实数。
为实数。
(i)求证:函数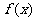 具有性质
具有性质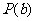 ; (ii)求函数
; (ii)求函数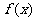 的单调区间。
的单调区间。
(2)已知函数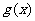 具有性质
具有性质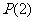 。给定
。给定 设
设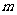 为实数,
为实数,
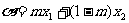 ,
,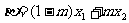 ,且
,且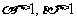 ,
,
若| |<|
|<| |,求
|,求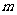 的取值范围。
的取值范围。
[解析] 本小题主要考查函数的概念、性质、图象及导数等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分16分。
(1)(i)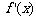
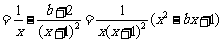
∵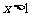 时,
时,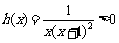 恒成立,
恒成立,
∴函数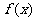 具有性质
具有性质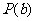 ;
;
(ii)(方法一)设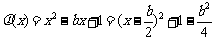 ,
,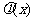 与
与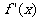 的符号相同。
的符号相同。
当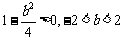 时,
时,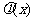
 ,
,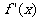
 ,故此时
,故此时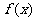 在区间
在区间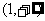 上递增;
上递增;
当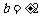 时,对于
时,对于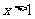 ,有
,有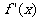
 ,所以此时
,所以此时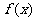 在区间
在区间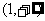 上递增;
上递增;
当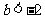 时,
时,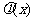 图像开口向上,对称轴
图像开口向上,对称轴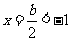 ,而
,而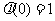 ,
,
对于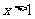 ,总有
,总有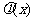
 ,
,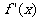
 ,故此时
,故此时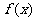 在区间
在区间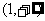 上递增;
上递增;
(方法二)当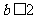 时,对于
时,对于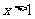 ,
,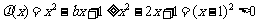
所以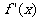
 ,故此时
,故此时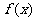 在区间
在区间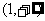 上递增;
上递增;
当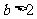 时,
时,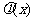 图像开口向上,对称轴
图像开口向上,对称轴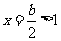 ,方程
,方程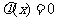 的两根为:
的两根为: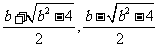 ,而
,而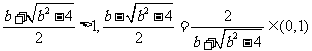
当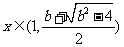 时,
时,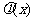
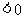 ,
,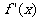
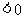 ,故此时
,故此时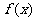 在区间
在区间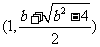 上递减;同理得:
上递减;同理得: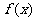 在区间
在区间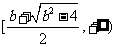 上递增。
上递增。
综上所述,当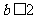 时,
时,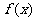 在区间
在区间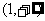 上递增;
上递增;
当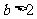 时,
时,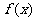 在
在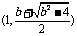 上递减;
上递减;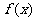 在
在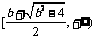 上递增。
上递增。
(2)(方法一)由题意,得: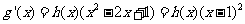
又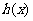 对任意的
对任意的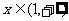 都有
都有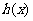 >0,
>0,
所以对任意的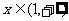 都有
都有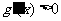 ,
,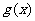 在
在 上递增。
上递增。
又 。
。
当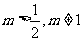 时,
时, ,且
,且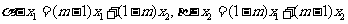 ,
,
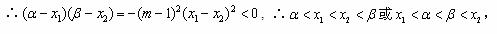
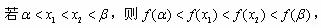
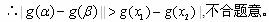
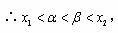

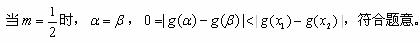
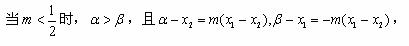
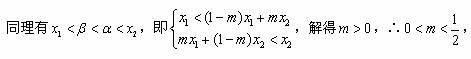
综合以上讨论,得:所求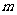 的取值范围是(0,1)。
的取值范围是(0,1)。
(方法二)由题设知,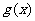 的导函数
的导函数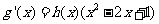 ,其中函数
,其中函数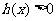 对于任意的
对于任意的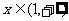 都成立。所以,当
都成立。所以,当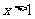 时,
时,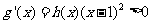 ,从而
,从而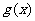 在区间
在区间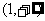 上单调递增。
上单调递增。
①当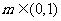 时,有
时,有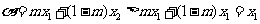 ,
,
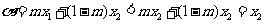 ,得
,得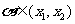 ,同理可得
,同理可得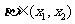 ,所以由
,所以由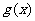 的单调性知
的单调性知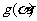 、
、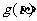
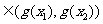 ,
,
从而有| |<|
|<| |,符合题设。
|,符合题设。
②当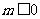 时,
时,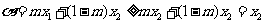 ,
,
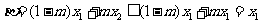 ,于是由
,于是由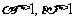 及
及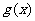 的单调性知
的单调性知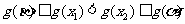 ,所以|
,所以| |≥|
|≥| |,与题设不符。
|,与题设不符。
③当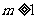 时,同理可得
时,同理可得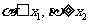 ,进而得|
,进而得| |≥|
|≥| |,与题设不符。
|,与题设不符。
因此综合①、②、③得所求的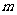 的取值范围是(0,1)。
的取值范围是(0,1)。
数学Ⅱ(附加题)
19、(本小题满分16分)
设各项均为正数的数列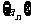 的前n项和为
的前n项和为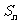 ,已知
,已知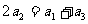 ,数列
,数列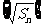 是公差为
是公差为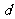 的等差数列。
的等差数列。
(1)求数列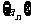 的通项公式(用
的通项公式(用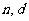 表示);
表示);
(2)设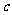 为实数,对满足
为实数,对满足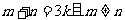 的任意正整数
的任意正整数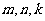 ,不等式
,不等式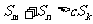 都成立。求证:
都成立。求证: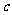 的最大值为
的最大值为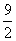 。
。
[解析] 本小题主要考查等差数列的通项、求和以及基本不等式等有关知识,考查探索、分析及论证的能力。满分16分。
(1)由题意知: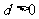 ,
, 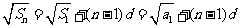
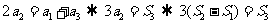 ,
,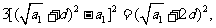
化简,得: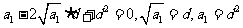
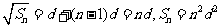 ,
,
当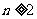 时,
时,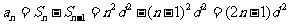 ,适合
,适合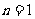 情形。
情形。
故所求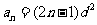
(2)(方法一)
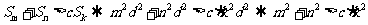 ,
, 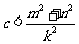 恒成立。
恒成立。
又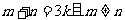 ,
,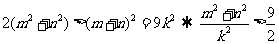 ,
,
故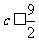 ,即
,即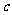 的最大值为
的最大值为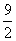 。
。
(方法二)由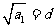 及
及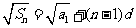 ,得
,得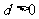 ,
,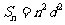 。
。
于是,对满足题设的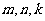 ,
,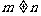 ,有
,有
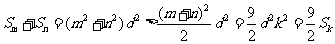 。
。
所以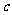 的最大值
的最大值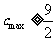 。
。
另一方面,任取实数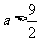 。设
。设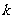 为偶数,令
为偶数,令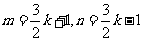 ,则
,则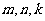 符合条件,且
符合条件,且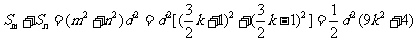 。
。
于是,只要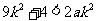 ,即当
,即当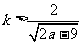 时,
时,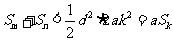 。
。
所以满足条件的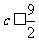 ,从而
,从而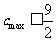 。
。
因此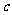 的最大值为
的最大值为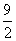 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com