
18、(本小题满分16分)
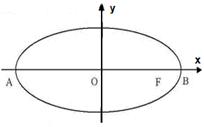 在平面直角坐标系
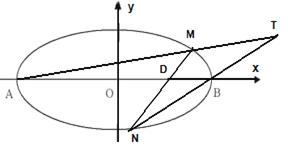
在平面直角坐标系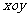 中,如图,已知椭圆
中,如图,已知椭圆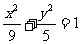 的左、右顶点为A、B,右焦点为F。设过点T(
的左、右顶点为A、B,右焦点为F。设过点T(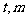 )的直线TA、TB与椭圆分别交于点M
)的直线TA、TB与椭圆分别交于点M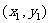 、
、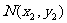 ,其中m>0,
,其中m>0,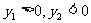 。
。
(1)设动点P满足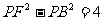 ,求点P的轨迹;
,求点P的轨迹;
(2)设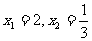 ,求点T的坐标;
,求点T的坐标;
(3)设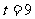 ,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
[解析] 本小题主要考查求简单曲线的方程,考查方直线与椭圆的方程等基础知识。考查运算求解能力和探究问题的能力。满分16分。
(1)设点P(x,y),则:F(2,0)、B(3,0)、A(-3,0)。
由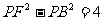 ,得
,得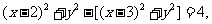 化简得
化简得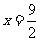 。
。
故所求点P的轨迹为直线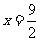 。
。
(2)将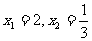 分别代入椭圆方程,以及
分别代入椭圆方程,以及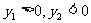 得:M(2,
得:M(2,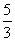 )、N(
)、N(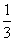 ,
,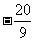 )
)
直线MTA方程为: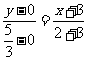 ,即
,即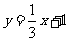 ,
,
直线NTB 方程为: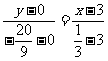 ,即
,即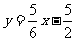 。
。
 联立方程组,解得:
联立方程组,解得: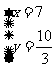 ,
,
所以点T的坐标为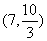 。
。
(3)点T的坐标为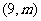
直线MTA方程为: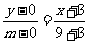 ,即
,即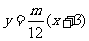 ,
,
直线NTB 方程为: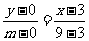 ,即
,即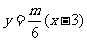 。
。
分别与椭圆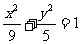 联立方程组,同时考虑到
联立方程组,同时考虑到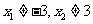 ,
,
解得: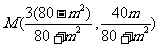 、
、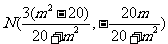 。
。
(方法一)当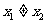 时,直线MN方程为:
时,直线MN方程为: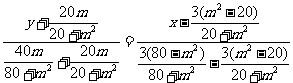
令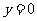 ,解得:
,解得: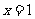 。此时必过点D(1,0);
。此时必过点D(1,0);
当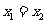 时,直线MN方程为:
时,直线MN方程为: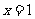 ,与x轴交点为D(1,0)。
,与x轴交点为D(1,0)。
所以直线MN必过x轴上的一定点D(1,0)。
(方法二)若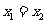 ,则由
,则由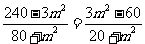 及
及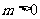 ,得
,得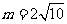 ,
,
此时直线MN的方程为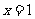 ,过点D(1,0)。
,过点D(1,0)。
若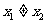 ,则
,则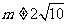 ,直线MD的斜率
,直线MD的斜率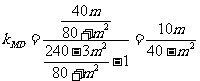 ,
,
直线ND的斜率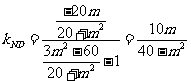 ,得
,得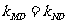 ,所以直线MN过D点。
,所以直线MN过D点。
因此,直线MN必过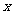 轴上的点(1,0)。
轴上的点(1,0)。
17、(本小题满分14分)
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=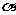 ,∠ADE=
,∠ADE=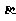 。
。
(1)该小组已经测得一组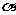 、
、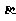 的值,tan
的值,tan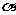 =1.24,tan
=1.24,tan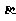 =1.20,请据此算出H的值;
=1.20,请据此算出H的值;
(2)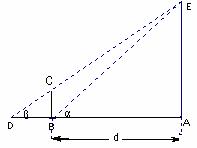 该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使
该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使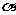 与
与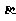 之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,
之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,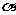 -
-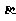 最大?
最大?
[解析] 本题主要考查解三角形的知识、两角差的正切及不等式的应用。
(1)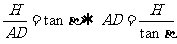 ,同理:
,同理: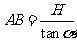 ,
,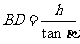 。
。
AD—AB=DB,故得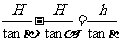 ,解得:
,解得: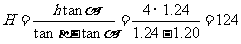 。
。
因此,算出的电视塔的高度H是124m。
(2)由题设知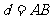 ,得
,得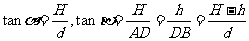 ,
,

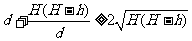 ,(当且仅当
,(当且仅当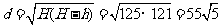 时,取等号)
时,取等号)
故当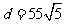 时,
时,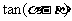 最大。
最大。
因为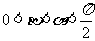 ,则
,则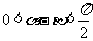 ,所以当
,所以当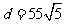 时,
时,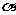 -
-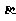 最大。
最大。
故所求的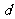 是
是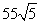 m。
m。
16、(本小题满分14分)
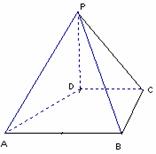
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
[解析] 本小题主要考查直线与平面、平面与平面的位置关系,考查几何体的体积,考查空间想象能力、推理论证能力和运算能力。满分14分。
(1)证明:因为PD⊥平面ABCD,BC 平面ABCD,所以PD⊥BC。
平面ABCD,所以PD⊥BC。
由∠BCD=900,得CD⊥BC,
又PD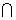 DC=D,PD、DC
DC=D,PD、DC 平面PCD,
平面PCD,
所以BC⊥平面PCD。
因为PC 平面PCD,故PC⊥BC。
平面PCD,故PC⊥BC。
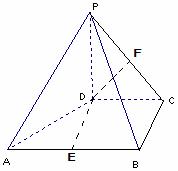 (2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
(2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF=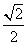 ,故点A到平面PBC的距离等于
,故点A到平面PBC的距离等于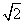 。
。
(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得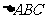 的面积
的面积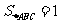 。
。
由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积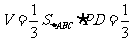 。
。
因为PD⊥平面ABCD,DC 平面ABCD,所以PD⊥DC。
平面ABCD,所以PD⊥DC。
又PD=DC=1,所以 。
。
由PC⊥BC,BC=1,得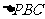 的面积
的面积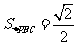 。
。
由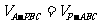 ,
,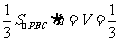 ,得
,得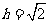 ,
,
故点A到平面PBC的距离等于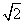 。
。
15、(本小题满分14分)
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(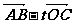 )·
)·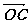 =0,求t的值。
=0,求t的值。
[解析]本小题考查平面向量的几何意义、线性运算、数量积,考查运算求解能力。满分14分。
(1)(方法一)由题设知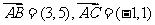 ,则
,则
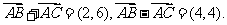
所以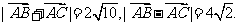
故所求的两条对角线的长分别为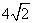 、
、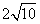 。
。
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的两条对角线的长分别为BC=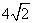 、AD=
、AD=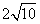 ;
;
(2)由题设知: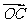 =(-2,-1),
=(-2,-1),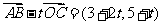 。
。
由(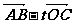 )·
)·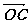 =0,得:
=0,得: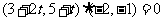 ,
,
从而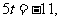 所以
所以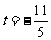 。
。
 或者:
或者: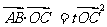 ,
,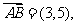
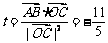
14、将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是____▲____。
,则S的最小值是____▲____。
[答案]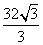
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小正三角形的边长为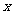 ,则:
,则: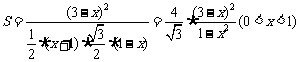
(方法一)利用导数求函数最小值。
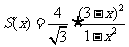 ,
,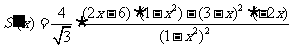

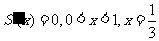 ,
,
当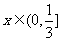 时,
时,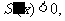 递减;当
递减;当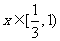 时,
时,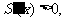 递增;
递增;
故当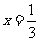 时,S的最小值是
时,S的最小值是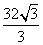 。
。
(方法二)利用函数的方法求最小值。
令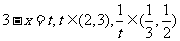 ,则:
,则: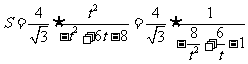
故当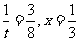 时,S的最小值是
时,S的最小值是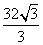 。
。
13、在锐角三角形ABC,A、B、C的对边分别为a、b、c,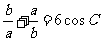 ,则
,则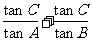 =____▲_____。
=____▲_____。
[答案]4
[解析] 考查三角形中的正、余弦定理三角函数知识的应用,等价转化思想。一题多解。
(方法一)考虑已知条件和所求结论对于角A、B和边a、b具有轮换性。
当A=B或a=b时满足题意,此时有: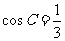 ,
,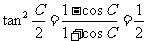 ,
,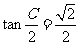 ,
,
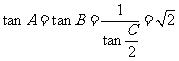 ,
,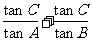 = 4。
= 4。
(方法二)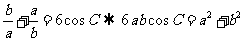 ,
,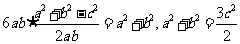
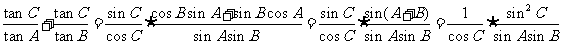 由正弦定理,得:上式=
由正弦定理,得:上式=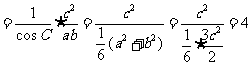
12、设实数x,y满足3≤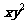 ≤8,4≤
≤8,4≤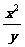 ≤9,则
≤9,则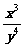 的最大值是 ▲ 。。来源
的最大值是 ▲ 。。来源
[答案]27
[解析] 考查不等式的基本性质,等价转化思想。
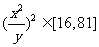 ,
,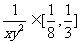 ,
,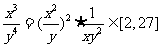 ,
,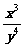 的最大值是27。
的最大值是27。
11、已知函数 ,则满足不等式
,则满足不等式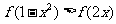 的x的范围是__▲___。
的x的范围是__▲___。
[答案]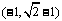
[解析] 考查分段函数的单调性。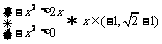
10、定义在区间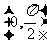 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
[答案]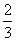
[解析] 考查三角函数的图象、数形结合思想。线段P1P2的长即为sinx的值,
且其中的x满足6cosx=5tanx,解得sinx=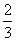 。线段P1P2的长为
。线段P1P2的长为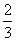
9、在平面直角坐标系xOy中,已知圆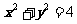 上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是______▲_____[来源
上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是______▲_____[来源
[答案](-13,13)
[解析]考查圆与直线的位置关系。 圆半径为2,
圆心(0,0)到直线12x-5y+c=0的距离小于1,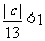 ,
,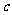 的取值范围是(-13,13)。
的取值范围是(-13,13)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com