
18.(本小题满分8分)
 高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
|
分组 |
频数 |
频率 |
|
[85,95) |
① |
② |
|
[95,105) |
|
0.050 |
|
[105,115) |
|
0.200 |
|
[115,125) |
12 |
0.300 |
|
[125,135) |
|
0.275 |
|
[135,145) |
4 |
③ |
|
[145,155) |
|
0.050 |
|
合计 |
|
④ |
(1)根据上面图表,①②③④处的数值分别为 , , , ;
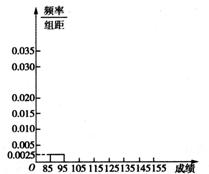
 (2)在所给的坐标系中画出[85,155]的频率分布直方图;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
[解析](1)①1;②0.025;③ 0.1;④1…………3分
(2)频率分布直方图如图. ………………………5分
(2)利用组中值算得平均数为:90×0.025 + 100×0.05 + 110×0.2 + 120×0.3 + 130×0.275 + 140×0.1 + 150×0.05 = 122.5;
故总体落在[129,155]上的概率为
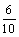 ×0.275 + 0.1 + 0.05 = 0.315.
………………………8分
×0.275 + 0.1 + 0.05 = 0.315.
………………………8分
17.(本小题满分8分)
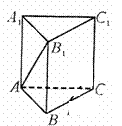 如图,在正三棱柱
如图,在正三棱柱 中,已知
中,已知 .
.
(1)求正三棱柱 的体积;
的体积;
(2)直线 所成角的正弦值.
所成角的正弦值.
[解析](1)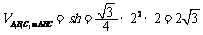 . …………3分
. …………3分
(2)令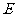 为
为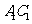 中点,连
中点,连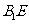 ,则
,则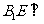 面
面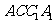 .
.
再连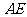 ,得
,得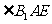 为
为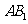 与面
与面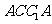 所成角.…………… 6分
所成角.…………… 6分
在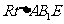 中,
中,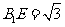 ,
,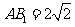 ,
,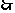
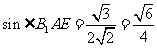 .
.
故直线 所成角的正弦值
所成角的正弦值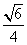 . ………………………8分
. ………………………8分
16.(本小题满分6分)
心脏跳动时,血压在增加或减小.心脏每完成一次跳动,血压就完成一次改变,血压的最大值和最小值分别为收缩压和舒张压.设某人的血压满足函数关系式P (t)
= 95 + A sin ,其中P (t)为血压(mmHg),t为时间(min),其函数图象如图所示.
,其中P (t)为血压(mmHg),t为时间(min),其函数图象如图所示.
 (1)根据图象写出该人的血压随时间变化的函数解析式;
(1)根据图象写出该人的血压随时间变化的函数解析式;
(2)求出该人的收缩压,舒张压及每分钟心跳的次数.
[解析](1)由图象可知,振幅A = 120 – 95 = 25,
周期T =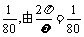 ,知
,知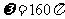 ,于是
,于是
P (t)
= 95 + 25 sin160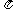 t. ………………………3分
t. ………………………3分
(2)收缩压为95 + 25 = 120(mmHg);
舒张压为95 – 25 = 70 (mmHg),
心跳次数为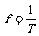 = 80次.………………………6分
= 80次.………………………6分
15.当x、y满足条件 时,目标函数z = x+3y的最大值为_____12_____.
时,目标函数z = x+3y的最大值为_____12_____.
[解析]在直角坐标系内画出可行域为△OAB(O为原点),A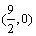 ,B(3,3),由图可知,最优解为B (3,3),故Zmax = 12.
,B(3,3),由图可知,最优解为B (3,3),故Zmax = 12.
14.已知 的三边长分别为
的三边长分别为 ,则
,则 的值为
的值为 .
.
[解析]由余弦定理得,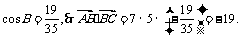
13.如果 ,
,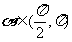 ,那么
,那么 等于
等于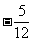 .
.
[解析]由已知得,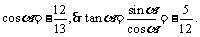
12.甲,乙两人在相同条件下练习射击,每人打 发子弹,命中环数如下
发子弹,命中环数如下
|
甲 |
6 |
8 |
9 |
9 |
8 |
|
乙 |
10 |
7 |
9 |
7 |
7 |
如果选择甲、乙二人中的一个去参加比赛,你应选择____甲______.
[解析]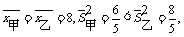 故选甲.
故选甲.
11.一个盒子中装有3个完全相同的小球,分别标以号码1,2,3,从中任取一球,则取出2号球的概率是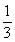 .
.
10.若 是
是 的三边,直线
的三边,直线 与圆
与圆 相离,则
相离,则 一定是
( C )
一定是
( C )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
[解析]由已知得,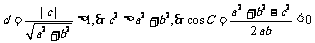 ,故
,故 是钝角三角形.
是钝角三角形.
9.设a,b表示两条不同的直线, 表示平面,则以下命题正确的有
(
A )
表示平面,则以下命题正确的有
(
A )
① ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
A. ①② B. ①②③ C. ②③④ D. ①②④
[解析]易知①②正确;对于③,b可能在 内;对于④,a可能平行平面
内;对于④,a可能平行平面 ,故选A.
,故选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com