
21.(本题12分)
椭圆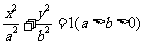 与直线
与直线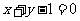 相交于
相交于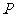 、
、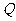 两点,且
两点,且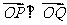 (
(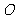 为坐标原点).
为坐标原点).
(Ⅰ)求证: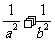 等于定值;
等于定值;
(Ⅱ)当椭圆的长轴长为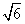 时,求出椭圆的标准方程,并判断焦点与以短轴为直径的圆的位置关系;
时,求出椭圆的标准方程,并判断焦点与以短轴为直径的圆的位置关系;
(Ⅲ)当椭圆的离心率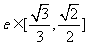 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.
20.(本题12分)
已知数列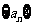 的前三项依次为
的前三项依次为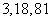 ,且
,且 是等比数列.
是等比数列.
(Ⅰ)证明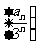 是等差数列;
是等差数列;
(Ⅱ)试求数列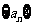 的前
的前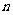 项和
项和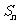 .
.
19.(本题12分)
|
 (Ⅰ)证明:AB1⊥BC1;
(Ⅰ)证明:AB1⊥BC1;
(Ⅱ)求点B到平面AB1C1的距离;
(Ⅲ)求二面角C1-AB1-A1的大小.
18.(本题12分)
2010年5月1日,上海世博会将举行,在安全保障方面,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为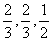 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。
(1)求A能够入选的概率;
(2)规定:每有1人入选,则相应的训练基地得到3000元的训练经费,否则得不到训练经费,求该基地得到训练经费恰为6000元的概率。
17.(本题10分)
设函数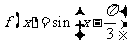 .
.
(Ⅰ)若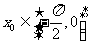 ,且
,且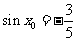 ,求
,求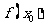 的值;
的值;
(Ⅱ)将函数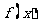 的图象向左平移
的图象向左平移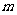 个单位,使平移后的图象关于
个单位,使平移后的图象关于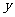 轴对称,若
轴对称,若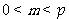 ,求
,求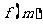 的值.
的值.
16.设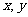 满足约束条件
满足约束条件 ,若目标函数
,若目标函数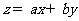 (a>0,b>0)的值的最大值为12,则
(a>0,b>0)的值的最大值为12,则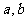 满足的关系为________
满足的关系为________
15.若球的内接正四棱锥的高为4,底面所在的平面截球所得的截面面积为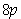 ,则球的体积为_________.
,则球的体积为_________.
14.定义在R上的函数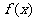 满足
满足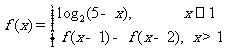 ,则
,则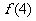 =_______
=_______
13.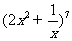 的展开式中
的展开式中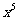 的系数是________
的系数是________
12.正三棱柱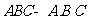 中,
中,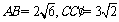 ,过
,过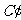 作与底面成60°二面角的截面与底边
作与底面成60°二面角的截面与底边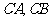 分别交于
分别交于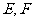 两点,则三棱锥
两点,则三棱锥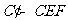 体积的最大值是
体积的最大值是
A.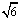 B.
B.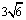 C.
C.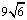 D.
D.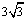
第Ⅱ卷(非选择题共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com