3.定义运算，已知，计算：=　　　　

2. 有一个六个面分别标上数字1、2、3、4、5、6的正方体，甲、乙、丙三位同学从不同的角度观察的结果如图所示．如果记2的对面的数字为m，3的对面的数字为n，则方程的解大致在区间，上，则　　　　 ．

1. 利用计算器，列出自变量和函数值的对应值如下表：

	0.2	0.6	1.0	1.4	1.8	2.2	2.6	3.0	3.4	…
	1.149	1.516	2.0	2.639	3.482	4.595	6.063	8.0	10.556	…
	0.04	0.36	1.0	1.96	3.24	4.84	6.76	9.0	11.56	…

那么方程的一个根位于下列区间的　　　　　

8. [解析]方程的根显然，原方程等价于，原方程的实根是曲线与曲线的交点的横坐标；而曲线是由曲线向上或向下平移个单位而得到的。若交点(x_i ,)(i＝1,2,…,k)均在直线y＝x的同侧，因直线y＝x与交点为：；所以结合图象可得：

三　范例剖析

例1　 已知a是实数，函数，如果函数在区间上有零点，求a的取值范围.

辨析：设二次函数，方程的两根和满足．(I)求实数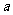的取值范围；(II)试比较与的大小．并说明理由．

例2　 在xOy平面上有一点列P₁( a₁, b₁ ), P₂( a₂,b₂ ),…,P_n ( a_n, b_n )…,对每个自然数n点P_n位于函数y = 2000 ()^x (0<a<1)的图象上，且点P_n，点 (n,0) 与点 (n+1,0) 构成一个以P_n为顶点的等腰三角形　 (1)求点P_n的纵坐标b_n的表达式；(2)若对于每个自然数n, 以b_n , b_n+1 , b_n+2为边长能构成一个三角形，求a的取值范围；(3)设C_n= lg( b_n ) (n∈N^*),若a取(2)中确定的范围内的最小整数，问数列{C_n}前多少项的和最大？试说明理由　

辨析：已知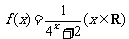，P₁(x₁,y₁)、P₂(x₂,y₂)是函数图象上两点，且线段

P₁P₂中点P的横坐标是．(1)求证点P的纵坐标是定值；(2)若数列的通项公式是

…m),求数列的前m项和S_m ；(3)在(2)的条件下，若

时，不等式恒成立，求实数a的取值范围

例3. 甲、乙两地相距S千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米／时，已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成：可变部分与速度 v(千米／时)的平方成正比，比例系数为b；固定部分为a元.

　① 把全程运输成本y(元)表示为速度v(千米／时)的函数，并指出函数的定义域；

　② 为了使全程运输成本最小，汽车应以多大速度行驶？　　

辨析：某工厂拟建一座底面为矩形、面积为200平方米且深为1米的无盖长方体的三级污水池(如图所示)如果池外圈四壁建造单价为每平方米400元，中间两条隔墙建造单价为每平方米248元，池底建造单价为每平方米80元。

　(1)试设计污水池底面的长和宽，使总造价最低，并求出最低造价；

　(2)由于受地形限制，地面的长、宽都不超过16米，试设计污水池底面的长和宽，使总

造价最低，并求出最低造价。

四　巩固训练

7. 解：当时，显然不成立

当时，因当即时结论显然成立；

当时只要即可

即，则.

6.

5. 解：画出与的图象有两个交点，故方程的实数解的个数为2个。

4. 解：依题意，有0<a<1且3a－1<0，解得0<a<，又当x<1时，(3a－1)x+4a>7a－1，当x>1时，log_ax<0，所以7a－1³0解得x³故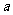的取值范围是

3. 解：由，函数有最小值可知a>1，所以不等式可化为x－1>1，即x>2.

2. 解：要使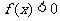，且，所以

，又，∴，故的取值范围是