18．(本小题满分13分)

解：(Ⅰ)∵　 ∴　 ………………1分

又函数处取得极值　 ∴①………………3分

又函数的图象与直线在点(1，0)处相切

∴② ………………………………………………………4分

③ ………………………………………………………………6分

由①②③解得：，，。……………………………………………7分

(Ⅱ)由(Ⅰ)可得：，　 ……8分

当时，，函数的单调递减区间为； …………………10分

当或时，，函数的单调递增区间为，。…13分

17．(本小题满分13分)

解：(Ⅰ)令，则展开式的各项系数和为 ………………………………3分

又展开式的各项二项式系数和为 ……………………………………………5分

∴即　 ………………………………………………………………6分

于是 ……………………………………………………………………………………7分

(Ⅱ)由(Ⅰ)可知：　 ∴展开式的中间两项二项式系数最大………9分

即 ……………………………………………11分

。 ………………………………………13分

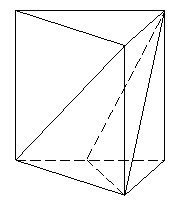
16．(本小题满分13分)

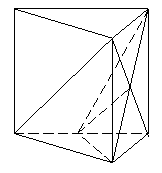(Ⅰ)证明：连结，令，则为的中点………1分

而为的中点　 ∴∥ ………………………………………………3分

又，

∴∥平面………………………………………………………………6分

(Ⅱ)解：由(Ⅰ)可知：∥

∴(或其补角)为异面直线与所成的角 …………………………………………………8分

又正三棱柱的所有棱长都为2，为的中点

∴，，，…………………………9分

在中， …………………………………11分

∴异面直线与所成的角为。 ……………………………………………………………13分

11．　　　 12．　　　 13．　　　 14．　　　 15．，

21．(本小题满分12分)已知函数，，函数

在、处取得极值，其中。

(Ⅰ)求实数的取值范围；

(Ⅱ)判断在上的单调性；

(Ⅲ)已知在上的最大值比最小值大 　，若方程有3个不同的解，

求实数的取值范围。

参考解答及评分意见

20．(本小题满分12分)如图，已知四棱锥，底面为菱形，⊥平面，，、分别是、的中点。

(Ⅰ)证明：⊥；

(Ⅱ)若为上的动点，与平面所成最大角的正切值为，求二面角的余弦值。

19．(本小题满分12分)甲、乙两人进行一种游戏，两人同时随机地喊出杠、虎、鸡、虫，按照

杠打虎、虎吃鸡、鸡吃虫、虫啃杠的原则决定胜负。 (比如甲喊杠的同时，乙若喊虎则乙输，乙若

喊虫则乙赢，乙若喊杠或鸡则不分胜负。)　 若两人同时喊出一次后不分胜负则继续喊下去，直到

分出胜负。

(Ⅰ)喊一次甲就获胜的概率是多少？

(Ⅱ)甲在喊不超过三次的情况下就获胜的概率是多少？

18．(本小题满分13分)已知函数处取得极值，并且它的图象

与直线在点(1，0)处相切。

(Ⅰ)求、、的值；

(Ⅱ)求函数的单调区间。

17．(本小题满分13分)已知的展开式中，名项系数的和与其各项二项式系数的和之比为32。

(Ⅰ)求；

(Ⅱ)求展开式中二项式系数最大的项。　　　　　　

16．(本小题满分13分)如图，正三棱柱的所有棱长都为2，为的中点。

(Ⅰ)求证：∥平面；

(Ⅱ)求异面直线与所成的角。