
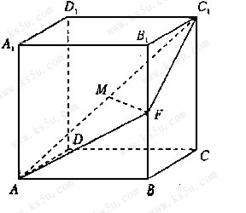
19.(天津市天津一中2010届高三第四次月考文科)已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1
的中点, M为线段AC1的中点.
(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1;
(3)求平面AFC1与与平面ABCD所成二面角的大小.
19、解:(1)取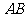 中点M,连接
中点M,连接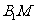 ,
,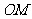
则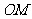
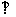 平面
平面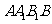 ,则
,则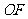 在平面
在平面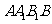 内的摄影为
内的摄影为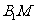 ,……………………(2分)
,……………………(2分)
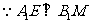
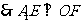 ……………………(4分)
……………………(4分)
(2)由体积转换可求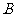 点到平面
点到平面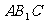 的距离为
的距离为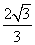 ,……………………(7分)
,……………………(7分)
而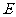 是
是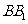 的中点
的中点
所以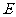 点到平面
点到平面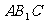 的距离为
的距离为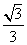 ……………………(8分)
……………………(8分)
(3)取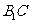 的中点
的中点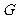 ,连接
,连接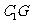 ,则
,则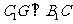 ,又
,又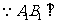 平面
平面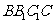
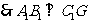
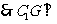 平面
平面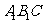 ,作
,作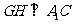 于
于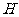 ,连接
,连接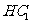
所以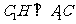
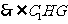 是所求二面角的平面角……………………(10分)
是所求二面角的平面角……………………(10分)
易得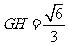 ,又
,又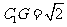
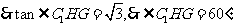
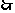 所求二面角的平面角为
所求二面角的平面角为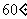 ……………………(12分)
……………………(12分)
另解:空间向量方法
(1)同上……………………(4分)
(2)如图,以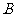 点为坐标原点,分别以
点为坐标原点,分别以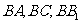 所在直线为
所在直线为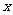 轴,
轴,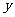 轴,
轴,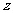 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则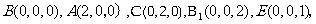
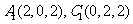 ……(5分)
……(5分)
设平面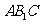 的法向量为
的法向量为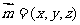
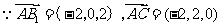
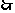 求得平面
求得平面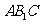 的法向量为
的法向量为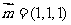 ……………………(6分)
……………………(6分)
又
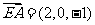
所以,点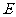 到平面
到平面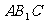 的距离
的距离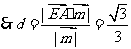 ……………………(8分)
……………………(8分)
(3)设平面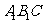 的法向量为
的法向量为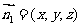
可求得平面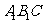 的法向量为
的法向量为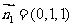 ……………………(9分)
……………………(9分)
同理可求得平面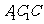 的法向量为
的法向量为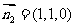 ……………………(10分)
……………………(10分)
所以,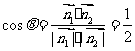 ……………………(11分)
……………………(11分)
所以二面角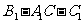 的大小为
的大小为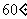 ……………………(12分)
……………………(12分)
19.(天津市天津一中2010届高三第四次月考理科)如图,在直三棱柱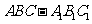 中,
中,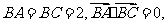 异面直线
异面直线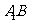 与
与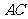 成
成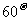 的角,点
的角,点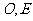 分别是棱
分别是棱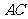 和
和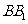 的中点,点
的中点,点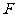 是棱
是棱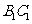 上的动点。
上的动点。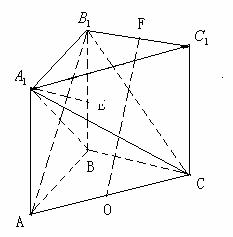
(1)证明: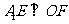 ;
;
(2)求点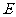 到平面
到平面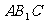 的距离;
的距离;
(3)求二面角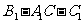 的大小。
的大小。
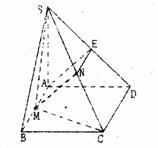
19.(I)证明:取SD中点E,连接AE,NE,
 则
则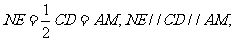
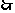 四边形AMNE为平行四边形,
四边形AMNE为平行四边形,
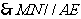 …………1分
…………1分
又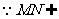 平面SAD …………3分
平面SAD …………3分
(2)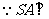 平面ABCD,
平面ABCD,
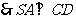 ,
,
 底面ABCD为矩形,
底面ABCD为矩形,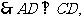
又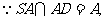
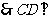 平面SAD,
平面SAD,
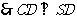
 即为二面角S-CD-A的平面角,
即为二面角S-CD-A的平面角,
即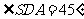 …………5分
…………5分
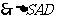 为等腰直角三角形,
为等腰直角三角形,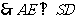
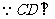 平面SAD,
平面SAD,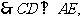
又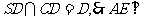 平面SCD
平面SCD
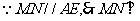 平面SCD,
平面SCD,
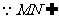 平面SMC,
平面SMC,
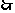 平面SMC
平面SMC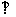 平面SCD …………8分
平面SCD …………8分
(3)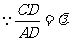 ,设AD=SA=a,则CD
,设AD=SA=a,则CD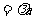
由(2)可得MN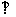 平面SCD,
平面SCD,
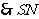 即为SM在平面SCD内的射影
即为SM在平面SCD内的射影
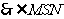 即为直线SM与平面SCD所成角,
即为直线SM与平面SCD所成角,
即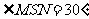 …………9分
…………9分
而MN=AE=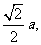
 中,
中,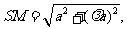 而
而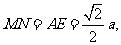 [
[
 中,由
中,由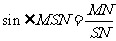 得
得
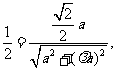 解得
解得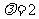
当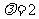 时,直线SM与平面SCD所成角为
时,直线SM与平面SCD所成角为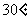 …………12分
…………12分
19.(天津市六校2010届高三第三次联考文科)(本小题满分12分)
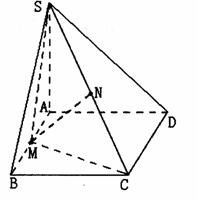
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥平面ABCD,二面角S-
CD-A的平面角为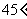 ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.
(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SCD;
 (3)若
(3)若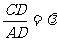 ,求实数
,求实数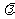 的值,使得直线SM与平面SCD所成角为
的值,使得直线SM与平面SCD所成角为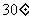
19.解:(I)当点E为BC的中点时,EF与平面PAC平行.
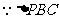 中,E、F分别为BC、PB的中点.
中,E、F分别为BC、PB的中点.
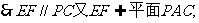
而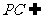 平面PAC,
平面PAC,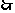 EF//平面PAC …………4分
EF//平面PAC …………4分
(II)证明: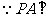 平面ABCD,BE
平面ABCD,BE 平面ABCD,
平面ABCD,
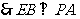
又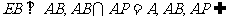 平面PAB,
平面PAB,
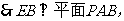
又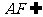 平面PAB,
平面PAB,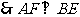
又PA=PB=1,点F是PB的中点,
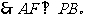 [
[
又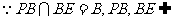 PBE,
PBE,
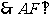 平面PBE.
平面PBE.
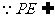 平面PBE,
平面PBE,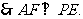 …………8分
…………8分
(3)过A作AG⊥DE于G,连PG,
又∵DE⊥PA,则DE⊥平面PAG,
则∠PGA是二面角P-DE-A的二面角,
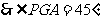 ,
,
∵PD与平面ABCD所成角是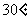 ,
,
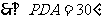
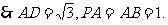
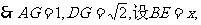
则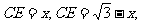
在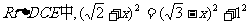 ,
,
得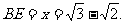 …………12分
…………12分
注:其它方法可参考本题标准
19.(天津市六校2010届高三第三次联考理科)(本小题12分)
如图,PA⊥ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在 边BC上移动.
(I)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(II)证明:无论点E在边BC的何处,都有PE⊥AF;
(III)当BE等于何值时,二面角P-DE-A的大小为45°.
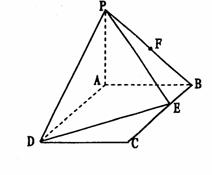
20.(天津市武清区2009-2010学年高三下学期第一次模拟文)(本小题满分12分)
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=600,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点。
(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
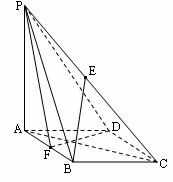 (3)求BE与平面PAC所成的角。
(3)求BE与平面PAC所成的角。
证明:(1)取PD中点为M,连ME,MF ∵ E是PC的中点 ∴ ME是△PCD的中位线
∴ ME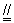
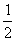 CD ∵ F是AB中点且由于ABCD是菱形,AB
CD ∵ F是AB中点且由于ABCD是菱形,AB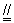 CD[
CD[
∴ ME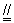 FB ∴ 四边形MEBF是平行四边形 …………2分
FB ∴ 四边形MEBF是平行四边形 …………2分
∴ BE∥MF …………………3分
∵ BE 平面PDF ,MF
平面PDF ,MF 平面PDF ∴ BE∥平面PDF
………4分
平面PDF ∴ BE∥平面PDF
………4分
(2) ∵ PA⊥平面ABCD
DF 平面ABCD ∴ DF⊥PA……………5分
平面ABCD ∴ DF⊥PA……………5分
∵ 底面ABCD是菱形,∠BAD=600 ∴ △DAB为正△
∵ F是AB中点 ∴ DF⊥AB ……………6分
∵ PA、AB是平面PAB内的两条相交直线 ∴ DF⊥平面PAB ………7分
∵ DF 平面PDF ∴ 平面PDF⊥平面PAB ………………8分
平面PDF ∴ 平面PDF⊥平面PAB ………………8分
(3)连BD交AC与O、连EO ∵ 底面ABCD是菱形 ∴ BO⊥AC
∵ PA⊥平面ABCD
BO 平面ABCD ∴ BO⊥PA
平面ABCD ∴ BO⊥PA
∵ PA、AC是平面PAC内的两条相交直线 ∴ BO⊥平面PAC …………9分
∴ EO是BE在平面PAC内的射影
∴ ∠BEO是BE与平面PAC所成的角 ………………10分
∵ O是AC、BD的中点 ∴ BO=1,EO是△PAC的中位线 ∴ EO=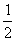 PA=1
PA=1
∴ 在直角△BEO中,tan∠BEO=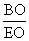 =1 ∴ ∠BEO=450
=1 ∴ ∠BEO=450
∴ 直线BE与平面PAC所成的角为450 …………………12分
19.(天津市武清区2009-2010学年高三下学期第一次模拟理)(本小题满分12分)
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=600,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点。
(1)求证:BE∥平面PDF;
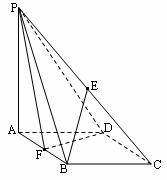 (2)求证:平面PDF⊥平面PAB;
(2)求证:平面PDF⊥平面PAB;
(3)求平面PAB与平面PCD所成的锐角。
证明:(1)取PD中点为M,连ME,MF ∵ E是PC的中点 ∴ ME是△PCD的中位线
∴ ME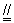
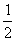 CD ∵ F是AB中点且由于ABCD是菱形,AB
CD ∵ F是AB中点且由于ABCD是菱形,AB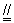 CD
CD
∴ ME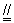 FB ∴ 四边形MEBF是平行四边形 …………2分
FB ∴ 四边形MEBF是平行四边形 …………2分
∴ BE∥MF …………………3分
∵ BE 平面PDF ,MF
平面PDF ,MF 平面PDF ∴ BE∥平面PDF
………4分
平面PDF ∴ BE∥平面PDF
………4分
(2)∵ PA⊥平面ABCD
DF 平面ABCD ∴ DF⊥PA ……………5分
平面ABCD ∴ DF⊥PA ……………5分
∵ 底面ABCD是菱形,∠BAD=600 ∴ △DAB为正△
∵ F是AB中点 ∴ DF⊥AB ……………6分
∵ PA、AB是平面PAB内的两条相交直线 ∴ DF⊥平面PAB ………7分
∵ DF 平面PDF ∴ 平面PDF⊥平面PAB ………………8分
平面PDF ∴ 平面PDF⊥平面PAB ………………8分
(3)(解法一)以A为原点,垂直于AD、AP的方向为x轴,AD、AP的方向分别为y轴、z轴建立空间直角坐标系,易知P(0,0,1)、C(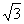 ,3,0)、D(0,2,0)、
,3,0)、D(0,2,0)、
F(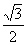 ,
,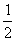 ,0)…………………9分
,0)…………………9分
由(2)知DF⊥平面PAB,
∴ 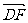 =(
=(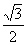 ,-
,-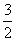 ,0)是平面PAB的一个法向量 …………10分
,0)是平面PAB的一个法向量 …………10分
设平面PCD的一个法向量为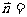 (x,y,z)
(x,y,z)
由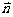 ·
·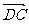 =(x,y,z)·(
=(x,y,z)·(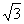 ,1,0)=0得
,1,0)=0得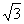 x+y=0
x+y=0
由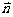 ·
·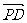 =(x,y,z)·(0,2,-1)=0得2y-z=0
=(x,y,z)·(0,2,-1)=0得2y-z=0
在以上二式中令y=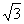 ,则得x=-1,z=2
,则得x=-1,z=2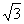
∴ 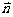 =(-1,
=(-1,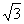 ,2
,2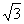 ) …………………11分
) …………………11分
设平面PAB与平面PCD所成的锐角为θ
∴ cosθ=|cos<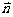 ,
,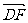 >|=
>|=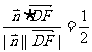
∴θ=600 ∴ 平面PAB与平面PCD所成的锐角为600 …………12分
(3)(解法二)设平面PAB与平面PCD的交线为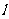 ,
,
∵ CD∥AB,AB 平面PAB,CD
平面PAB,CD 平面PAB ∴ CD∥平面PAB
平面PAB ∴ CD∥平面PAB
∵ CD 平面PCD ∴ CD∥
平面PCD ∴ CD∥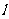 ∴ AB∥
∴ AB∥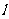 ……………9分
……………9分
作FM⊥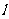 交
交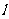 于M,连MD,易知FM=AP=1 ,DF=
于M,连MD,易知FM=AP=1 ,DF=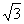 …………10分
…………10分
由(2)知DF⊥AB ∴ 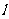 ⊥DF
⊥DF
∵ FM、DF是平面MDF内的两条相交直线,∴ 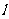 ⊥平面MDF
⊥平面MDF
∴ ∠FMD就是平面PAB与平面PCD所成的锐二面角的平面角 …………11分
在直角△FMD中,tan∠FMD=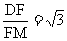
∴ ∠FMD=600
∴ 平面PAB与平面PCD所成的锐角为600 …………………12分
19.(本小题满分12分)解法一 向量法
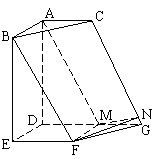
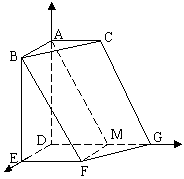 由已知,AD、DE、DG两两垂直,建立如图的坐标系,
由已知,AD、DE、DG两两垂直,建立如图的坐标系,
则A(0,0,2),B(2,0,2),C(0,1,2),
E(2,0,0),G(0,2,0),F(2,1,0)
(Ⅰ)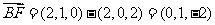
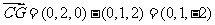
∴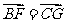 ,所以BF∥CG.
,所以BF∥CG.
又BF 平面ACGD
平面ACGD
故 BF//平面ACGD……………………4分]
(Ⅱ)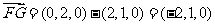 ,
,
设平面BCGF的法向量为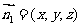 ,
,
则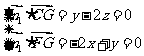 ,
,
令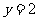 ,则
,则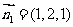 ,
,
而平面ADGC的法向量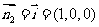
∴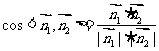 =
=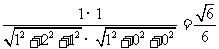
 故二面角D-CG-F的余弦值为
故二面角D-CG-F的余弦值为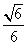 .……………………8分
.……………………8分
(Ⅲ)设DG的中点为M,连接AM、FM,
则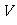 =
=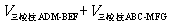
=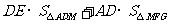 =
=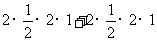 =
=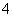 .……………12分
.……………12分
解法二设DG的中点为M,连接AM、FM,
则由已知条件易证四边形DEFM是平行四边形,
所以MF//DE,且MF=DE
又∵AB//DE,且AB=DE ∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,
又BF 平面ACGD
平面ACGD
故 BF//平面ACGD……………4分
(利用面面平行的性质定理证明,可参照给分)
(Ⅱ)由已知AD⊥面DEFG∴DE⊥AD ,DE⊥DG
即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则]
显然∠MNF是所求二面角的平面角.
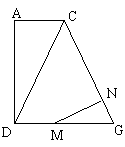 ∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴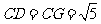 , ∴MN=
, ∴MN=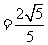
在直角三角形MNF中,MF=2,MN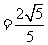
∴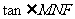 =
=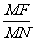 =
=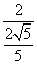 =
=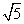 ,
,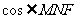 =
=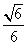
故二面角D-CG-F的余弦值为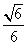 ……………………8分
(Ⅲ)
……………………8分
(Ⅲ)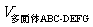 =
=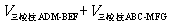 =
=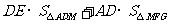 =
=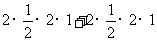 =
= .……………12分
.……………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com