
9.《秋菊打官司》的主要故事情节是:20世纪80年代,已有身孕的秋菊在其丈夫被村长踢伤丧失了劳动能力后,她历经艰辛,最终把村长告上了法庭,村长终被拘留。下列说法不正确的是
A.它反映了秋菊运用法律手段,捍卫了自己的合法权利
B.它反映了当时实行的村民民主自治制度保障了人民当家作主的权利
C.它反映了新的历史时期,我国公民的法制意识明显增强了
D.它反映了新的历史时期,我国的法制建设取得了很大成就
8.右图是一幅关于抗日战争的漫画。对此漫画所表达的主
题,理解最准确的是
A.中国经济实力强于日本
B.全民族抗战是抗战胜利的重要保证
C.中国抗战是正义的反侵略战争
D.日本侵略势力付出了沉重代价
7.某课题组在探究“社会主义运动”课题过程中,整理了下列相关信息,你认为错误是
A.《共产党宣言》的发表,标志着马克思主义的诞生
B.巴黎公社是无产阶级建立政权的第一次伟大尝试
C.十月革命胜利使社会主义从理想变为现实
 D.开国大典标志着社会主义制度在中国建立
D.开国大典标志着社会主义制度在中国建立
6.2008年北京奥运会圆满结束(2001年我国申奥成功),可是大约一百年前(1901年),西方列强给中华民族送来了一份令人难以忍受的新世纪贺礼是
A.火烧圆明园 B.割占宝岛台湾
C.签订《辛丑条约》 D.提出“二十一条”
4.马克思说:“罗马到处都由罗马法官根据罗马法进行判决,从而使地方上的社会秩序都被宣布无效……”对这段话的准确理解
A.法官是罗马帝国的最高统治者 B.法官滥用权力,造成社会秩序混乱
C.罗马法官建立了罗马帝国 D.罗马法稳固了帝国的政治和经济基础
 A、义和团运动把斗争矛头直指在华洋教势力
A、义和团运动把斗争矛头直指在华洋教势力
B、反映民族矛盾是当时中国社会的主要矛盾
C、表达了义和团反对外来侵略的坚决态度
D、对清政府不再抱有幻想,依靠自身力量进行反侵略斗争
3.古往今来,无论是东方古国,或是西方近代国家,都以建章立制来强化中央对地方的的关系。下列具有此类性质的文献和制度是
①秦汉郡县制 ②十二铜表法 ③英国《权利法案》④美国《1787年宪法》
A.①② B.①④ C.③④ D.②③
2.“今我朝罢丞相,设五府、六部、都察院、通政司、大理寺等衙门,分理天下庶务,彼此颉颃,不敢相压。事皆朝廷总之,所以稳当。”(《皇明祖训》),材料所反映的有效历史信息是 A.明朝时期天下庶务繁多 B.由于废除丞相,造成部门众多,工作效率不高 C. 丞相制度的废除意味着君主专制发展 D.明朝时期由于君主不理政事,造成大权旁落
1.《左传•昭公七年》:“天有十日,人有十等。下所以事上,上所以共神也。故王臣公,公臣大夫,大夫臣士,士臣皂”。上述材料反映了西周社会结构的基本特点是
A.严格的等级关系 B.嫡长子拥有继承特权
C.通过垄断神权强化王权 D.血缘纽带和政治关系紧密结合
例6. 求证:以抛物线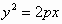 过焦点的弦为直径的圆,必与此抛物线的准线相切。
过焦点的弦为直径的圆,必与此抛物线的准线相切。
证明:如图5,设抛物线的准线为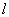 ,过A、B两点分别作AC、BD垂直于
,过A、B两点分别作AC、BD垂直于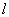 ,垂足分别为C、D。取线段AB中点M,作MH垂直
,垂足分别为C、D。取线段AB中点M,作MH垂直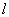 于H。
于H。
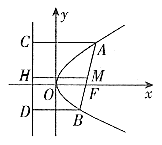
图5
由抛物线的定义有: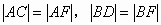
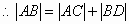
∵ABDC是直角梯形
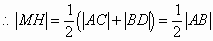
即 为圆的半径,而准线过半径MH的外端且与半径垂直,故本题得证。
为圆的半径,而准线过半径MH的外端且与半径垂直,故本题得证。
抛物线与面积问题
抛物线与面积相结合的题目是近年来中考数学中常见的问题。解答此类问题时,要充分利用抛物线和面积的有关知识,重点把握相交坐标点的位置及坐标点之间的距离,得出相应的线段长或高,从而求解。
例1. 如图1,二次函数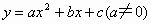 的图像与x轴交于A、B两点,其中A点坐标为(-1,0)。点C(0,5)、点D(1,8)在抛物线上,M为抛物线的顶点。
的图像与x轴交于A、B两点,其中A点坐标为(-1,0)。点C(0,5)、点D(1,8)在抛物线上,M为抛物线的顶点。
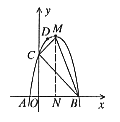
图1
(1)求抛物线的解析式;
(2)求△MCB的面积。
解:(1)设抛物线的解析式为
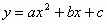 ,根据题意得
,根据题意得
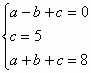 ,解得
,解得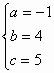
∴所求的抛物线的解析式为
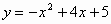
(2)∵C点坐标为(0,5),∴OC=5
令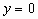 ,则
,则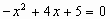 ,
,
解得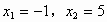
∴B点坐标为(5,0),OB=5
∵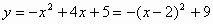 ,
,
∴顶点M的坐标为(2,9)
过点M作MN⊥AB于点N,
则ON=2,MN=9
∴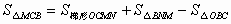
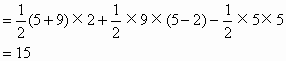
例2. 如图2,面积为18的等腰直角三角形OAB的一条直角边OA在x轴上,二次函数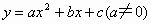 的图像过原点、A点和斜边OB的中点M。
的图像过原点、A点和斜边OB的中点M。
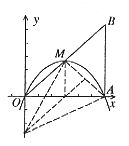
图2
(1)求出这个二次函数的解析式和对称轴。
(2)在坐标轴上是否存一点P,使△PMA中PA=PM,如果存在,写出P点的坐标,如果不存在,说明理由。
解:(1)∵等腰直角△OAB的面积为18,
∴OA=OB=6
∵M是斜边OB的中点,
∴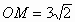
∴点A的坐标为(6,0)
点M的坐标为(3,3)
∵抛物线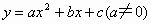
∴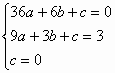 ,解得
,解得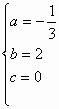
∴解析式为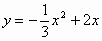 ,
,
对称轴为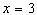
(2)答:在x轴、y轴上都存在点P,使△PAM中PA=PM。
①P点在x轴上,且满足PA=PM时,点P坐标为(3,0)。
②P点在y轴上,且满足PA=PM时,点P坐标为(0,-3)。
例3. 二次函数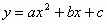 的图像一部分如图3,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。
的图像一部分如图3,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。
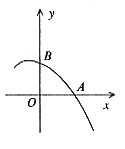
图3
(1)请判断实数a的取值范围,并说明理由。
(2)设此二次函数的图像与x轴的另一个交点为c,当△AMC的面积为△ABC面积的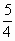 倍时,求a的值。
倍时,求a的值。
解:(1)由图象可知: ;图象过点(0,1),所以c=1;图象过点(1,0),则
;图象过点(0,1),所以c=1;图象过点(1,0),则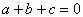 ;
;
当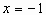 时,应有
时,应有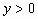 ,则
,则
当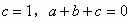 代入
代入
得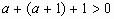 ,即
,即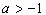
所以,实数a的取值范围为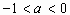 。
。
(2)此时函数 ,
,
要使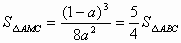
 ,
,
可求得 。
。
例4. 如图4,在同一直角坐标系内,如果x轴与一次函数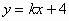 的图象以及分别过C(1,0)、D(4,0)两点且平行于y轴的两条直线所围成的图形ABDC的面积为7。
的图象以及分别过C(1,0)、D(4,0)两点且平行于y轴的两条直线所围成的图形ABDC的面积为7。

图4
(1)求K的值;
(2)求过F、C、D三点的抛物线的解析式;
(3)线段CD上的一个动点P从点D出发,以1单位/秒的速度沿DC的方向移动(点P不重合于点C),过P点作直线PQ⊥CD交EF于Q。当P从点D出发t秒后,求四边形PQFC的面积S与t之间的函数关系式,并确定t的取值范围。
解:(1)∵点A、B在一次函数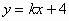 的图象上,
的图象上,
∴
且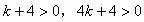
∵四边形ABDC的面积为7
∴
∴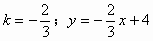 。
。
(2)由F(0,4),C(1,0),D(4,0)得
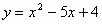
(3)∵PD=1×t=t
∴OP=4-t
∴
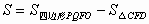
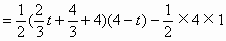
即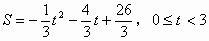 。
。
抛物线
1已知抛物线D:y2=4x的焦点与椭圆Q: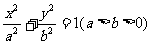 的右焦点F1重合,且点
的右焦点F1重合,且点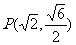 在椭圆Q上。(Ⅰ)求椭圆Q的方程及其离心率;(Ⅱ)若倾斜角为45°的直线l过椭圆Q的左焦点F2,且与椭圆相交于A,B两点,求△ABF1的面积。
在椭圆Q上。(Ⅰ)求椭圆Q的方程及其离心率;(Ⅱ)若倾斜角为45°的直线l过椭圆Q的左焦点F2,且与椭圆相交于A,B两点,求△ABF1的面积。
解:(Ⅰ)由题意知,抛物线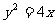 的焦点为(1,0)
的焦点为(1,0)
∴椭圆Q的右焦点F1的坐标为(1,0)。∴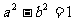 ①
①
又点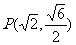 在椭圆Q上, ∴
在椭圆Q上, ∴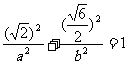 即
即 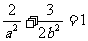 ②
②
由①②,解得 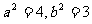 ∴椭圆Q的方程为
∴椭圆Q的方程为 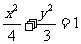 ∴离心离
∴离心离 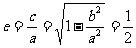
(Ⅱ)由(Ⅰ)知F2(-1,0)∴直线l的方程为 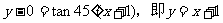 设
设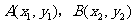 由方程组
由方程组 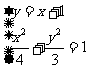 消y整理,得
消y整理,得 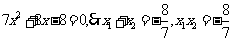 ∴
∴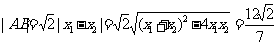
又点F1到直线l的距离 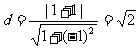 ∴
∴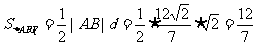
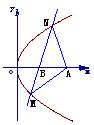 2如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为
2如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为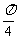 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积
的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积
解法一 由题意,可设l的方程为y=x+m,其中-5<m<0
由题意,可设l的方程为y=x+m,其中-5<m<0 由方程组
由方程组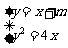 ,消去y,得x2+(2m-4)x+m2=0 ①∵直线l与抛物线有两个不同交点M、N,∴方程①的判别式Δ=(2m-4)2-4m2=16(1-m)>0,解得m<1,又-5<m<0,∴m的范围为(-5,0)
,消去y,得x2+(2m-4)x+m2=0 ①∵直线l与抛物线有两个不同交点M、N,∴方程①的判别式Δ=(2m-4)2-4m2=16(1-m)>0,解得m<1,又-5<m<0,∴m的范围为(-5,0)
设M(x1,y1),N(x2,y2)则x1+x2=4-2m,x1·x2=m2,∴|MN|=4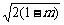
 点A到直线l的距离为d=
点A到直线l的距离为d=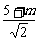

∴S△=2(5+m)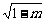 ,从而S△2=4(1-m)(5+m)2=2(2-2m)·(5+m)(5+m)≤2(
,从而S△2=4(1-m)(5+m)2=2(2-2m)·(5+m)(5+m)≤2(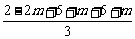 )3=128
)3=128
∴S△≤8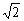 ,当且仅当2-2m=5+m,即m=-1时取等号
,当且仅当2-2m=5+m,即m=-1时取等号 故直线l的方程为y=x-1,△AMN的最大面积为8
故直线l的方程为y=x-1,△AMN的最大面积为8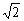

解法二 由题意,可设l与x轴相交于B(m,0),
l的方程为x = y +m,其中0<m<5
由题意,可设l与x轴相交于B(m,0),
l的方程为x = y +m,其中0<m<5
由方程组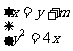 ,消去x,得y 2-4 y -4m=0 ①∵直线l与抛物线有两个不同交点M、N,
,消去x,得y 2-4 y -4m=0 ①∵直线l与抛物线有两个不同交点M、N,
∴方程①的判别式Δ=(-4)2+16m=16(1+m)>0必成立,设M(x1,y1),N(x2,y2)则y 1+ y 2=4,y 1·y 2=-4m,
∴S△=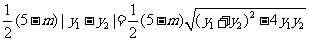 =4
=4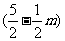
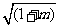 =4
=4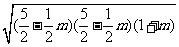
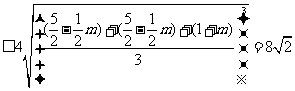 ∴S△≤8
∴S△≤8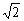 ,当且仅当
,当且仅当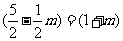 即m=1时取等号
即m=1时取等号
故直线l的方程为y=x-1,△AMN的最大面积为8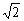

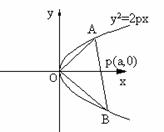 3已知O为坐标原点,P(
3已知O为坐标原点,P(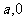 )(
)( )为
)为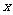 轴上一动点,过P作直线交抛物线
轴上一动点,过P作直线交抛物线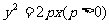 于A、B两点,设S△AOB=
于A、B两点,设S△AOB=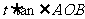 ,试问:
,试问: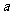 为何值时,t取得最小值,并求出最小值。
为何值时,t取得最小值,并求出最小值。
、解:交AB与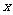 轴不重叠时,设AB的方程为
轴不重叠时,设AB的方程为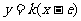
合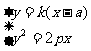 消y可得:
消y可得: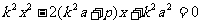
设A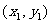 B
B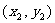 则
则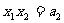 ,
, 交AB与x轴重叠时,上述结论仍然成立
交AB与x轴重叠时,上述结论仍然成立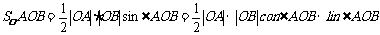 ∴
∴ 又
又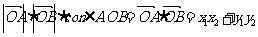 ∴
∴ ≥
≥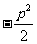 当
当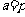 时 取“=”, 综上 当
时 取“=”, 综上 当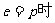

例5. 设P是抛物线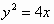 上的一个动点。
上的一个动点。
(1)求点P到点A(-1,1)的距离与点P到直线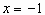 的距离之和的最小值;
的距离之和的最小值;
(2)若B(3,2),求 的最小值。
的最小值。
解:(1)如图3,易知抛物线的焦点为F(1,0),准线是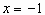
由抛物线的定义知:点P到直线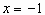 的距离等于点P到焦点F的距离。
的距离等于点P到焦点F的距离。
于是,问题转化为:在曲线上求一点P,使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小。
显然,连结AF交曲线于P点,则所求最小值为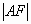 ,即为
,即为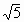 。
。
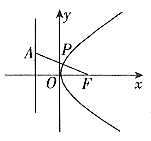
图3
(2)如图4,自点B作BQ垂直准线于Q交抛物线于点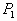 ,则
,则
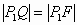 ,则有
,则有
即 的最小值为4
的最小值为4

图4
点评:本题利用抛物线的定义,将抛物线上的点到准线的距离转化为该点到焦点的距离,从而构造出“两点间线段距离最短”,使问题获解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com