
14.(2009宁夏海南卷理)等差数列{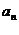 }前n项和为
}前n项和为 。已知
。已知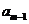 +
+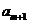 -
-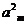 =0,
=0,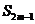 =38,则m=_______
=38,则m=_______
解析:由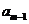 +
+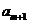 -
-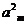 =0得到
=0得到 。
。
答案10
13.(2009辽宁卷理)等差数列 的前
的前 项和为
项和为 ,且
,且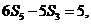 则
则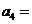
[解析]∵Sn=na1+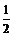 n(n-1)d w.w. ∴S5=5a1+10d,S3=3a1+3d ∴6S5-5S3=30a1+60d-(15a1+15d)=15a1+45d=15(a1+3d)=15a4[答案]
n(n-1)d w.w. ∴S5=5a1+10d,S3=3a1+3d ∴6S5-5S3=30a1+60d-(15a1+15d)=15a1+45d=15(a1+3d)=15a4[答案]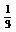
12.(2009全国卷Ⅱ理)设等差数列 的前
的前 项和为
项和为 ,若
,若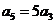 则
则 9 .
9 .
解: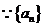 为等差数列,
为等差数列,
11.[答案]4 5 32
[解析](1)若 为偶数,则
为偶数,则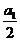 为偶, 故
为偶, 故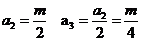
①当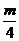 仍为偶数时,
仍为偶数时,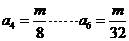 故
故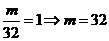
②当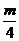 为奇数时,
为奇数时,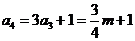
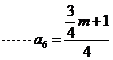 故
故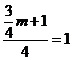 得m=4。
得m=4。
(2)若 为奇数,则
为奇数,则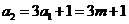 为偶数,故
为偶数,故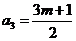 必为偶数
必为偶数
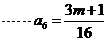 ,所以
,所以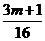 =1可得m=5
=1可得m=5
10.(2009湖北卷理)已知数列 满足:
满足: (m为正整数),
(m为正整数), 若
若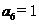 ,则m所有可能的取值为__________。
,则m所有可能的取值为__________。


9.(2009全国卷Ⅱ文)设等比数列{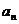 }的前n项和为
}的前n项和为 。若
。若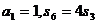 ,则
,则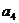 = ×
= ×
答案:3
解析:本题考查等比数列的性质及求和运算,由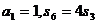 得q3=3故a4=a1q3=3。
得q3=3故a4=a1q3=3。
8.(2009山东卷文)在等差数列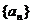 中,
中,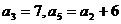 ,则
,则 .
.
[解析]:设等差数列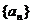 的公差为
的公差为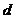 ,则由已知得
,则由已知得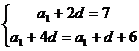 解得
解得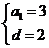 ,所以
,所以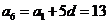 .
. 

答案:13.
[命题立意]:本题考查等差数列的通项公式以及基本计算.
7.(2009江苏卷)设 是公比为
是公比为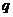 的等比数列,
的等比数列,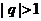 ,令
,令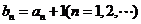 ,若数列
,若数列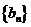 有连续四项在集合
有连续四项在集合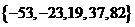 中,则
中,则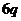 = .
= .
[解析] 考查等价转化能力和分析问题的能力。等比数列的通项。

 有连续四项在集合
有连续四项在集合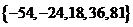 ,四项
,四项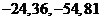 成等比数列,公比为
成等比数列,公比为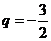 ,
,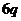 = -9
= -9
6.(2009北京理)已知数列 满足:
满足: 则
则 ________;
________; =_________.
=_________.
[答案]1,0
[解析]本题主要考查周期数列等基础知识.属于创新题型.
依题意,得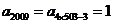 ,
,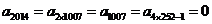 .
. 

∴应填1,0.
5.(2009北京文)若数列 满足:
满足: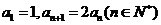 ,则
,则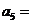 ;前8项的和
;前8项的和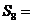
.(用数字作答)
.w[解析]本题主要考查简单的递推数列以及数列的求和问题.m 属于基础知识、基本运算的考查.
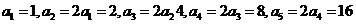 ,
,
易知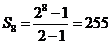 ,∴应填255.
,∴应填255.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com