19．(本小题满分12分)

　　 设函数f(x)＝(x+2)²－2ln(x+2)．

　　 (Ⅰ)求f(x)的单调区间；

(Ⅱ)若关于x的方程f(x)＝x²+3x+a在区间[－1，1]上只有一个实数根，求实数a的取

值范围．

18．(本小题满分12分)

　　 已知正三棱柱ABC－A₁B₁C₁的各条棱长都为a，P为A₁B上的点，且PC⊥AB．

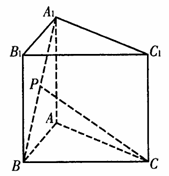　　 (Ⅰ)求二面角P－AC－B的正切值；

　　 (Ⅱ)求点B到平面PAC的距离．

17．(本小题满分12分)

　　 不透明盒中装有10个形状大小一样的小球，其中有2个小球上标有数字1，有3个小球上标有数字2，还有5个小球上标有数字3．取出一球记下所标数字后放回，再取一球记下所 标数字，共取两次．设两次取出的小球上的数字之和为ξ．

　　 (Ⅰ)求随机变量ξ的分布列；

　　 (Ⅱ)求随机变量ξ的期望Eξ．

16．(本小题满分12分)

　 已知函数f(x)＝2sin(x+)cos(x+)+2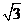cos²(x+)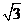－，α为常数.

(Ⅰ)求函数f(x)的周期；　 　

(Ⅱ)若0≤α≤π时，求使函数f(x)为偶函数的α值．

15．椭圆(a>b>0)的中心．右焦点．右顶点．及右准线与x轴的交点依次为O．

F．G．H，则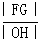的最大值为_________________.

14．设三棱锥的三个侧面两两互相垂直，且侧棱长均为2 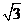，则其外接

球的表面积为______________________.

13．已知定义在R上的连续函数y＝f(x)的图象在点M(1,f(1))处

　　 的切线方程为y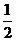＝－x+2，则f(1)+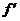(1)＝___________

12．已知函数f(x)，g(x)分别由右表给出，则f(g(1))＝______________．

11．某班级要从5名男生．3名女生中选派4人参加某次社区服务，如果要求至少有一名女

生，那么选派的4人中恰好有2名女生的概率为　　　　　　 。

10．数列a_n＝5×(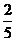)^2n－2 －4×(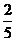)^n－1，(n ∈N﹡)，若a_p和a_q分别为数列中的最大项和最小项，则p+q＝

　　 A．3　　　　　　 　　　 B．4 　　　　　　　　 C．5　　　　　　　 D．6