
7.若复数 是纯虚数,则实数
是纯虚数,则实数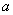 的值为(
)
的值为(
)
A.1
B.2
C.1或2 D.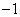
6.设 则复数
则复数 为实数的充要条件是
为实数的充要条件是
A. B.
B. C.
C. D.
D.
5.若复数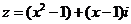 为纯虚数,则实数
为纯虚数,则实数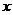 的值为
的值为
A.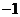 B.
B.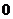 C.
C.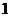 D.
D.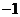 或
或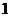
4.若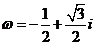 ,则等于
,则等于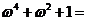 ( )
( )
A.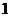 B.
B.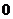 C.
C.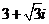 D.
D.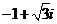
3.使复数为实数的充分而不必要条件是由 ( )
A.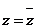 B.
B.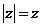 C.
C.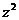 为实数
为实数  D.
D.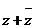 为实数
为实数
2.若有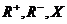 分别表示正实数集,负实数集,纯虚数集,则集合
分别表示正实数集,负实数集,纯虚数集,则集合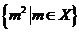 =( ).
=( ).
A.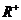 B.
B.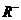 C.
C.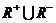 D.
D.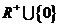
1.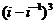 的虚部为( )
的虚部为( )
A.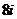 B.
B.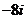 C.
C.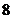 D.
D.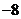
22.解:(1)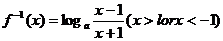
(2)设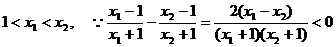
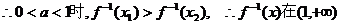 上是减函数;
上是减函数;
 上是增函数;
上是增函数;
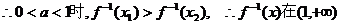 上是减函数;
上是减函数;
(3)当 上是减函数;
上是减函数;
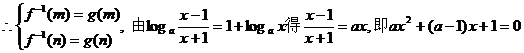
可知方程的两个根均大于1,即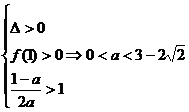
当a
> 1时,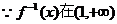 上是增函数;
上是增函数;
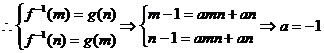 (舍去)
(舍去)
综上,得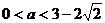
21. (1)令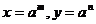 ,则
,则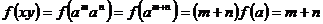 ,
,
同理, ,
,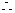 得证
得证
(2)任设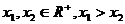 ,可令,
,可令,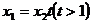 ,
,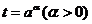 则
则

=
即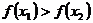
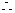
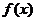 在正实数集上单调递增
在正实数集上单调递增
(3)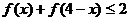 可化成,
可化成,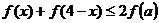
即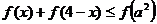 ,
,
即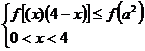 ,即
,即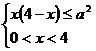 ,而当
,而当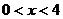 时,
时,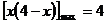 ,依题意,有
,依题意,有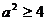 ,又
,又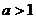
 .
.
19.(1)∵函数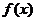 的图象关于原点对称,
的图象关于原点对称,
∴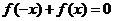 ,
,
有 ,
,
化简得 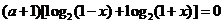 .
.
∵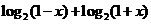 不恒为0,
不恒为0,
∴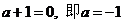 .
.
(2)由(1)得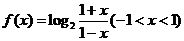 则
则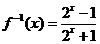 .
.
∵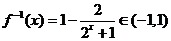
当
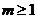 时,不等式
时,不等式 无解
无解
当
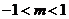 时,解不等式
时,解不等式 有
有
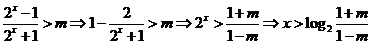 ;
;
当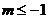 时,不等式
时,不等式 对任意的
对任意的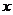 都成立,即
都成立,即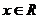 .
.
20(1)由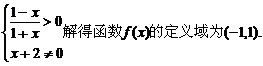
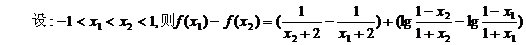
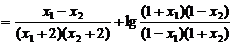 .又∵
.又∵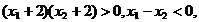
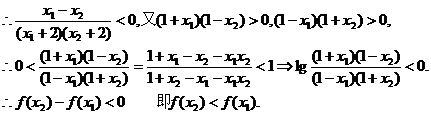
故函数f(x)在区间(-1,1)内是减函数.
(2)这里并不需要先求出f(x)的反函数f-1(x),再解方程f-1(x)=0
∵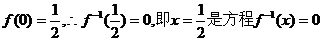 的一个解.
的一个解.
若方程f -1(x)=0还有另一解x0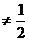 ,则
,则
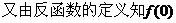
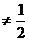 ,这与已知矛盾.
,这与已知矛盾.
故方程f -1(x)=0有唯一解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com