
5. 求解功率最大时要注意固定阻值与可变电阻的差异。
4. 输出功率大时效率不一定大,当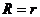 ,电源有最大输出功率时,效率仅为50%,所以功率大并不一定效率高。
,电源有最大输出功率时,效率仅为50%,所以功率大并不一定效率高。
3. 区分电源总功率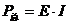 (消耗功率);
(消耗功率);
输出功率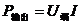 (外电路功率);
(外电路功率);
电源损耗功率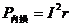 (内电路功率);
(内电路功率);
线路损耗功率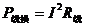
2. 在固定导体的I-U图线中,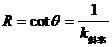 ,斜率越大,R越小;
,斜率越大,R越小;
在固定导体的U-I图线中,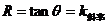 ,斜率越大,R越大,在闭合电路欧姆定律的U-I图象中,电源内阻
,斜率越大,R越大,在闭合电路欧姆定律的U-I图象中,电源内阻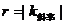 ,斜率越大,内阻r越大。
,斜率越大,内阻r越大。
例3. 如图3所示为一理想变压器,S为单刀双掷开关P为滑动变阻器的滑动触头,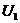 为加在初级线圈两端的电压,
为加在初级线圈两端的电压,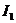 为初级线圈中的电流强度,则( )
为初级线圈中的电流强度,则( )
A. 保持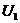 及P的位置不变,S由a合到b时,
及P的位置不变,S由a合到b时,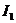 将增大
将增大
B. 保持P的位置及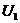 不变,S由b合到a时,R消耗的功率减小
不变,S由b合到a时,R消耗的功率减小
C. 保持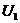 不变,S合在a处,使P上滑,
不变,S合在a处,使P上滑,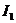 将增大
将增大
D. 保持P的位置不变,S合在a处,若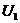 增大,
增大,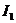 将增大
将增大
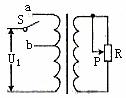
图3
解析:S由a合到b时,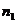 减小,由
减小,由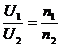 可知
可知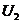 增大,
增大,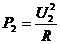 随之增大,而
随之增大,而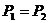 ,又
,又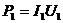 ,从而
,从而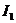 增大,可见选项A是正确的。当S由b合到a时,与上述情况相反,
增大,可见选项A是正确的。当S由b合到a时,与上述情况相反,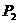 将减小,可见,选项B也是正确的。当P上滑时,R增大,
将减小,可见,选项B也是正确的。当P上滑时,R增大,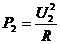 减小,又
减小,又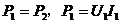 ,从而
,从而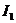 减小,可见选项C是错误的。当
减小,可见选项C是错误的。当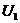 增大,由
增大,由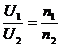 ,可知
,可知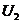 增大,
增大,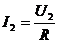 随之增大;由
随之增大;由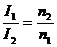 可知
可知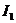 也增大,则选项D是正确的。
也增大,则选项D是正确的。
说明:在处理这类问题时,关键是要分清变量和不变量,弄清理想变压器中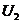 由
由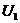 和匝数比决定;
和匝数比决定;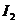 由
由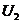 和负载电阻决定;
和负载电阻决定;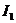 由
由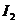 和匝数比决定。
和匝数比决定。
总结:变压器动态问题(制约问题)
①电压制约:当变压器原、副线圈的匝数比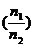 一定时,输出电压
一定时,输出电压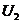 由输入电压决定,即
由输入电压决定,即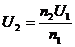 ,可简述为“原制约副”。
,可简述为“原制约副”。
②电流制约:当变压器原、副线圈的匝数比 一定,且输入电压
一定,且输入电压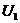 确定时,原线圈中的电流
确定时,原线圈中的电流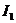 由副线圈中的输出电流
由副线圈中的输出电流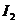 决定,即
决定,即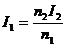 ,可简述为“副制约原”。
,可简述为“副制约原”。
③负载制约:变压器副线圈中的功率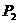 由用户负载决定,
由用户负载决定,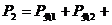 …;原线圈的输入功率
…;原线圈的输入功率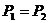 简述为“副制约原”。
简述为“副制约原”。
特例:当变压器空载时(即负载电阻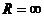 ),输出功率为零,输入电流为零,输入功率也为零。当副线圈短路时(即负载电阻R=0),输出电流为无穷大,则输入电流也是无穷大,使原线圈处于“短路”状态。
),输出功率为零,输入电流为零,输入功率也为零。当副线圈短路时(即负载电阻R=0),输出电流为无穷大,则输入电流也是无穷大,使原线圈处于“短路”状态。
[模型要点]
判断思路:
(1)电路中不论是串联还是并联部分,只要有一个电阻的阻值变大时,整个电路的总电阻就变大。只要有一个电阻的阻值变小时,整个电路的总电阻都变小。
(2)根据总电阻的变化,由闭合电路欧姆定律可判定总电流、电压的变化。
(3)判定变化部分的电流、电压变化。如变化部分是并联回路,那么仍应先判定固定电阻部分的电流、电压的变化,最后变化电阻部分的电流、电压就能确定了。
上述的分析方法俗称“牵一发而动全身”,其要点是从变量开始,由原因导出结果,逐层递推,最后得出题目的解。
图象特性
|
类型 |
公式 |
图象 |
特例 |
|
|
I-R图线 |
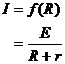 |
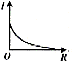 |
短路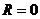 , ,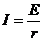 图象顶端 图象顶端 |
断路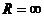 , ,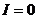 图象末端 图象末端 |
|
U-R图线 |
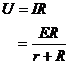 |
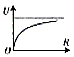 |
短路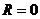 , ,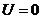 , ,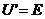 |
断路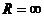 , ,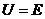 , ,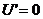 |
|
U-I图线 |
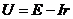 |
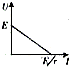 |
短路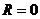 , ,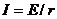 , ,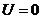 |
断路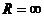 , ,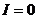 , ,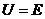 |
|
P-R图线 |
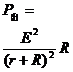 |
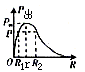 |
当R=r时,电源的输出功率最大,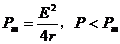 时有两个等效电阻 时有两个等效电阻 |
[误区点拨]
1. 区分固定导体的I-U图线与闭合电路欧姆定律的U-I图象。
2. 直流电路的动态变化引起的功能及图象问题
例2. 用伏安法测一节干电池的电动势和内电阻,伏安图象如图所示,根据图线回答:
(1)干电池的电动势和内电阻各多大?
(2)图线上a点对应的外电路电阻是多大?电源此时内部热耗功率是多少?
(3)图线上a、b两点对应的外电路电阻之比是多大?对应的输出功率之比是多大?
(4)在此实验中,电源最大输出功率是多大?
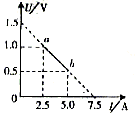
图2
解析:
(1)开路时(I=0)的路端电压即电源电动势,因此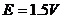 ,内电阻
,内电阻
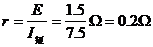
也可由图线斜率的绝对值即内阻,有:
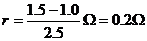
(2)a点对应外电阻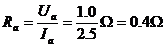
此时电源内部的热耗功率:
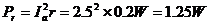
也可以由面积差求得:
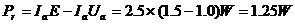
(3)电阻之比: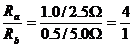
输出功率之比: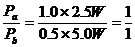
(4)电源最大输出功率出现在内、外电阻相等时,此时路端电压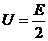 ,干路电流
,干路电流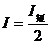 ,因而最大输出功率
,因而最大输出功率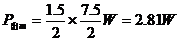
当然直接用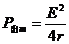 计算或由对称性找乘积IU(对应于图线上的面积)的最大值,也可以求出此值。
计算或由对称性找乘积IU(对应于图线上的面积)的最大值,也可以求出此值。
评点:利用题目给予图象回答问题,首先应识图(从对应值、斜率、截矩、面积、横纵坐标代表的物理量等),理解图象的物理意义及描述的物理过程:由U-I图象知E=1.5V,斜率表内阻,外阻为图线上某点纵坐标与横坐标比值;当电源内外电阻相等时,电源输出功率最大。
1. 直流电路的动态变化引起的电表读数变化问题
例1. 如图1所示电路中,当滑动变阻器的滑片P向左移动时,各表(各电表内阻对电路的影响均不考虑)的示数如何变化?为什么?
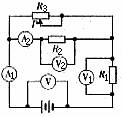
图1
解析:这是一个由局部变化而影响整体的闭合电路欧姆定律应用的动态分析问题。对于这类问题,可遵循以下步骤:先弄清楚外电路的串、并联关系,分析外电路总电阻怎样变化;由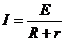 确定闭合电路的电流强度如何变化;再由
确定闭合电路的电流强度如何变化;再由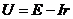 确定路端电压的变化情况;最后用部分电路的欧姆定律
确定路端电压的变化情况;最后用部分电路的欧姆定律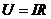 及分流、分压原理讨论各部分电阻的电流、电压变化情况。
及分流、分压原理讨论各部分电阻的电流、电压变化情况。
当滑片P向左滑动,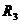 减小,即
减小,即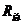 减小,根据
减小,根据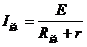 判断总电流增大,A1示数增大;
判断总电流增大,A1示数增大;
路端电压的判断由内而外,根据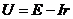 知路端电压减小,V示数减小;
知路端电压减小,V示数减小;
对R1,有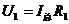 所以
所以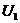 增大,
增大,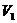 示数增大;
示数增大;
对并联支路,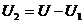 ,所以
,所以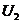 减小,
减小,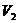 示数减小;
示数减小;
对R2,有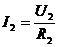 ,所以I2减小,A2示数减小。
,所以I2减小,A2示数减小。
评点:从本题分析可以看出,在闭合电路中,只要外电路中的某一电阻发生变化,这时除电源电动势、内电阻和外电路中的定值电阻不变外,其他的如干路中的电流及各支路的电流、电压的分配,从而引起功率的分配等都和原来的不同,可谓“牵一发而动全身”,要注意电路中各量的同体、同时对应关系,因此要当作一个新的电路来分析。解题思路为局部电路→整体电路→局部电路,原则为不变应万变(先处理不变量再判断变化量)。
15.⑴2I-+4H++MnO2=Mn2++2H2O+I2.
⑵ 2IO3-+5HSO3-=3H++5SO42-+H2O+I2 ; 氧化 ; 还原.
14. (1)不是 (2)25.94 LiF
13. (1) 2I -+ ClO-+2H+ = I2 + Cl- + H2O (2)I 2被 Na2SO3还原为I- ,
(3)SO32- + I2 +H2O = SO42- +2H++2I- (4) ClO-> I2 >SO42-
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com