
∴在 内
内 在
在 内
内
当 时, ∵
时, ∵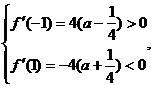
设 在
在 内的唯一极值点为
内的唯一极值点为 ,则
,则 ………………………………9分
………………………………9分
(Ⅱ) 由(Ⅰ)知当 时,
时,  在
在 是减函数,故没有极值点,从而
是减函数,故没有极值点,从而 …8分
…8分
故 在
在 内是减函数. …………………………………………………………………6分
内是减函数. …………………………………………………………………6分
∴在 内
内 , ………………………………………………………………………5分
, ………………………………………………………………………5分
又∵二次函数 的图象开口向上,
的图象开口向上,
∵ , ∴
, ∴ …………………………………………………………3分
…………………………………………………………3分
∴ ……………………………………………………………1分
……………………………………………………………1分
20,(Ⅰ) ∵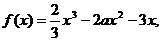
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com