
4.(本题满分10分)
有一种舞台灯,外形是正六棱柱,在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为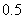 , 若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用ξ表示更换费用.
, 若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用ξ表示更换费用.
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出ξ的分布列,并求ξ的数学期望.
3.(本题满分10分)
已知矩阵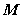
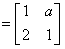 ,其中
,其中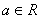 ,若点
,若点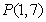 在矩阵
在矩阵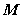 的变换下得到点
的变换下得到点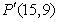 ,
,
(1)求实数a的值;
(2)求矩阵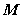 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
2.(本题满分10分)
设矩阵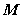 是把坐标平面上的点的横坐标伸长到3倍,纵坐标伸长到2倍的伸压变换矩阵.
是把坐标平面上的点的横坐标伸长到3倍,纵坐标伸长到2倍的伸压变换矩阵.
(1)求逆矩阵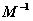 ;
;
(2)求椭圆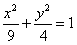 在矩阵
在矩阵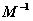 作用下变换得到的新曲线的方程.
作用下变换得到的新曲线的方程.
(总分40分,加试时间30分钟)
答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内.解答过程应写在答题卷的相应位置上,在其它地方答题无效.
1.(本题满分10分)
 已知二项式
已知二项式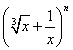 的展开式中各项系数和为256,
的展开式中各项系数和为256,
(1)求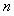 ;
(2)求展开式中的常数项.
;
(2)求展开式中的常数项.
20. (本题满分16分)已知函数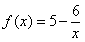 ,数列
,数列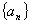 满足:
满足: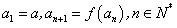
(1)若对于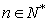 ,都有
,都有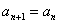 成立,求实数
成立,求实数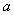 的值;
的值;
(2)若对于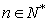 ,都有
,都有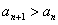 成立,求实数
成立,求实数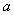 的取值范围;
的取值范围;
(3)请你构造一个无穷数列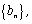 使其满足下列两个条件,并加以证明:
使其满足下列两个条件,并加以证明:
①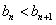 ,
,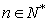 ;
;
②当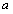 为
为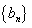 中的任意一项时,
中的任意一项时, 中必有某一项的值为1.
中必有某一项的值为1.
高 三 数 学 试 题
19.(本题满分16分)已知函数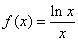
(1)求函数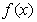 的单调区间;
的单调区间;
(2)设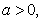 求函数
求函数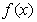 在
在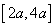 上的最小值;
上的最小值;
(3)某同学发现:总存在正实数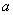 、
、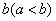 ,使
,使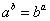 ,试问:他的判断是否正确?若不正确,请说明理由;若正确,请直接写出
,试问:他的判断是否正确?若不正确,请说明理由;若正确,请直接写出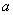 的取值范围(不需要解答过程).
的取值范围(不需要解答过程).
18.(本题满分15分)
已知数列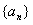 的前
的前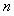 项和
项和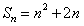 ,设数列
,设数列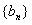 满足
满足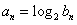 ,
,
(1)求数列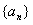 的通项公式;
的通项公式;
(2)求数列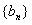 的前
的前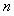 项和
项和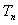 ;
;
(3)设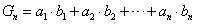 ,求
,求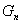 .
.
17. (本题满分15分)
已知集合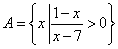 ,
,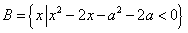
(1)当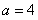 时,求
时,求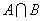 ;
;
(2)若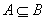 ,求实数
,求实数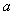 的取值范围.
的取值范围.
16.(本题满分14分)
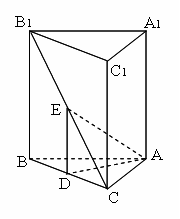
如图,在直三棱柱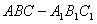 中,
中,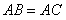 ,
,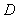 、
、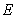 分别为
分别为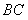 、
、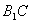 的中点,
的中点,
(1)求证: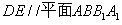 ;
;
(2)求证: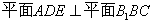
15.设函数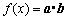 ,其中向量
,其中向量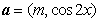 ,
,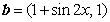 ,
,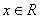 ,且
,且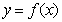 的图象经过点
的图象经过点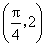 .
.
(1)求实数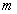 的值;
的值;
(2)求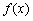 的最小正周期.
的最小正周期.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com