
4.16世纪晚期,山东某地开始出现“地多烟草、木棉转卖四方,五谷之利不及其半”的情况。这说明当时该地
①农业经济衰退 ②农业结构发生变化 ③商品经济发展 ④农产品加工业兴起
A.①② B.②③ C.③④ D.①③
3.据《东京梦华录》等记载,宋代都城多见“当街列床凳,堆垛冰雪”出售凉食和专向客商出租铺席宅舍等现象。这反映了
A.生活习俗改变 B.经商方式不受限制
C.官府鼓励经商 D.城市商业功能增强
2.清代一位军机大臣用一首诗来形容自己的工作:“依样胡芦画不难,胡芦变化有千端。画成依样旧胡芦,要把胡芦仔细看。”该诗直接说明了军机大臣 ( )
A.完全听命于皇帝,处理军国大事 B.在皇帝心目中没有任何地位
C.接替丞相职权,替皇帝处理政事 D.办事非常认真仔细
1.春秋时期,赵简子说“……克敌者,上大夫受县,下大夫受郡,士田十万,庶人工商遂”。这表明春秋时 ( )
A.世卿世禄的分封关系受到冲击 B.以郡统县的体制普遍建立
C.工商皆本思想出现 D.血缘政治隶属关系得到空前加强
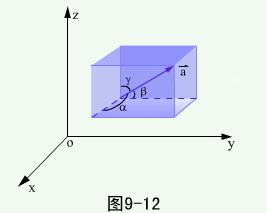
矢量  与
与  轴,
轴,  轴,
轴,  轴正向间夹角
轴正向间夹角 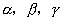 称为
称为  的方向角。它们的余弦
的方向角。它们的余弦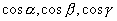 称为方向余弦。
称为方向余弦。
由投影定理有: 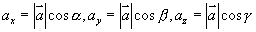
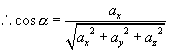 ,
, 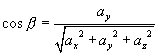 ,
,
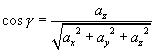
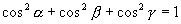 ,
,
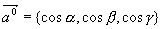
例1 设 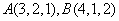 为空间两点,求
为空间两点,求 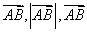 的方向余弦。
的方向余弦。
解 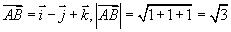
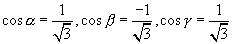
例2 设 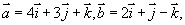 求
求 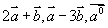
解 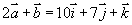 ,
, 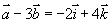
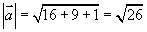
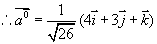
例3(定比分点坐标)设 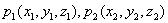 为两已知点,在连接
为两已知点,在连接 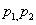 两点的直线上另有一点
两点的直线上另有一点 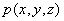 ,使有向线段
,使有向线段 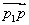 与
与 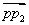 的长度之比为
的长度之比为 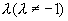 ,求p点坐标。
,求p点坐标。
解 由题意 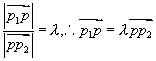
而 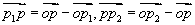
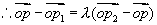 ,即
,即 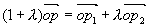
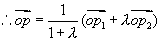
即 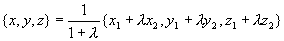
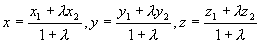
当 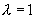 时,得中点坐标公式:
时,得中点坐标公式:
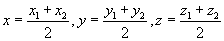
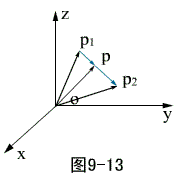
在空间直角坐标系中,设点 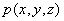 ,作矢量
,作矢量 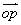 (矢径),则
(矢径),则 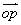 在
在 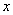 轴,
轴, 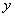 轴,
轴, 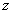 轴上的投影分别为
轴上的投影分别为 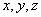 ,又设
,又设 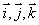 分别是与
分别是与 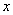 轴,
轴, 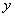 轴,
轴, 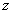 轴同方向的单位矢量(叫基本单位矢量),则
轴同方向的单位矢量(叫基本单位矢量),则
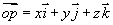
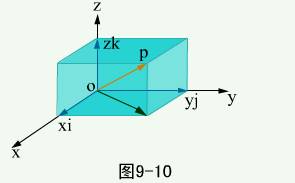
设点 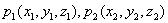 ,作矢量
,作矢量 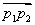 ,显然
,显然
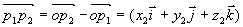
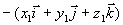
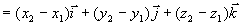
由以上讨论知:空间中任一矢量  ,可写成
,可写成
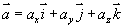
上式称为  的坐标表达式,
的坐标表达式, 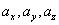 称为
称为  的坐标,它们分别是
的坐标,它们分别是  在
在  轴,
轴, 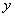 轴,
轴, 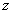 轴上的投影,所以
轴上的投影,所以  也可简记为
也可简记为
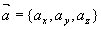
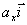 、
、 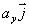 、
、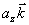 分别称为矢量
分别称为矢量 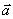 在x轴、y轴、z轴上的分矢量。显然有
在x轴、y轴、z轴上的分矢量。显然有
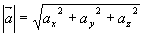
设 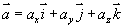 ,
, 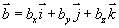 ,
,
则 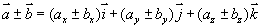 ,
,
即 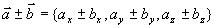
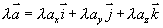
即 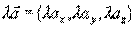
前面讲过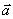 ∥
∥ 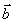 的充要条件是
的充要条件是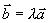 ,即
,即 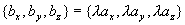 ,所以
,所以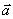 ∥
∥ 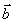 的充要条件是:
的充要条件是: 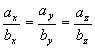
有向线段 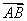 的值:
的值:
设 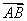 是数轴u上的有向线段(见图)
是数轴u上的有向线段(见图)
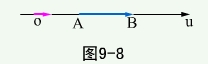
数 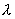 满足
满足 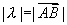 ,且
,且 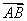 与u同向,
与u同向, 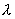 取正;
取正; 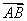 与u反向,
与u反向, 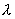 取负;称
取负;称 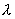 为u轴上有向线段
为u轴上有向线段 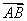 的值,记为AB。设
的值,记为AB。设 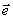 是与u轴同方向的单位矢量,则
是与u轴同方向的单位矢量,则
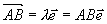
矢量 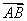 在数轴u上的投影:
在数轴u上的投影:
设矢量 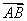 的起点A和终点B在数轴u上的投影分别为
的起点A和终点B在数轴u上的投影分别为 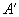 和
和 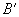 ,则u轴上有向线段
,则u轴上有向线段 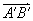 的值
的值 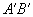 叫矢量
叫矢量 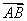 在数轴u上的投影,记作
在数轴u上的投影,记作 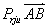 或
或 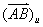
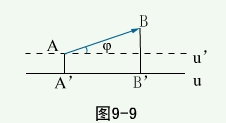
投影定理:矢量 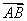 在轴u上的投影为
在轴u上的投影为
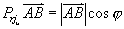
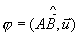
注: 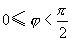 时,
时, 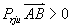 ;
; 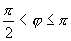 时,
时, 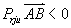 ;
; 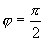 时,
时, 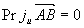 。
。
定理: 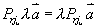 ,(
,( 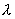 为常数)
为常数)
定理: 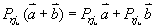
2.数与矢量的乘法
数 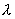 与矢量
与矢量  的乘积
的乘积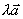 仍为矢量,其模
仍为矢量,其模 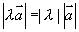 ,其方向为:
,其方向为: 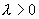 时,
时, 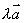 与
与  的方向相同;
的方向相同; 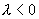 时,
时, 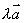 与
与  的方向相反;
的方向相反; 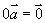 。
。
运算性质:(1) 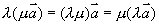
(2) 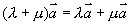
(3) 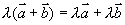
其中, 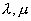 为常数。
为常数。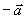
结论: (1)对任何非零矢量  ,有
,有 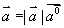 或
或 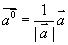
(2)设  、
、 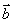 是两个非零矢量,则
是两个非零矢量,则 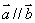 的充要条件是:存在唯
一的数
的充要条件是:存在唯
一的数 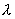 ,使
,使 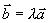 。
。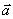
第三节 矢量的坐标表示
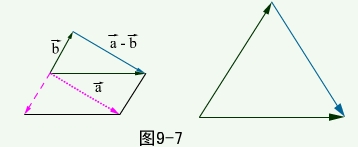
1. 加减法(平行四边形法则,三角形法则)
加减法(平行四边形法则,三角形法则)
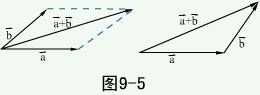
运算律: (1)交换律: 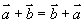
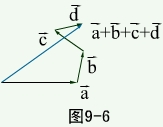
(2)结合律: 
减法 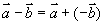
即有大小又有方向的量叫矢量(向量)。记作: 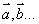 等,A为起点B为终点的矢量记为
等,A为起点B为终点的矢量记为 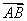 。
。
矢量的模:矢量的大小称为模,记 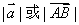 。
。
单位矢量:模为1的矢量叫单位矢量,与  方向相同的单位矢量记作
方向相同的单位矢量记作 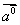 。
。
零矢量:模为0的矢量叫零矢量,记作 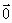 ,其方向不定。
,其方向不定。
矢量相等:模相等,方向相同的两个矢量  与
与 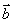 称为相等,记作:
称为相等,记作:
 =
= 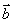 。
。
负矢量:与  的模相等,方向相反的矢量称为
的模相等,方向相反的矢量称为  的负矢量记作:–
的负矢量记作:– 。
。
自由矢量:与起点无关的矢量叫自由矢量。
两个非零矢量  与
与 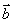 的夹角记为
的夹角记为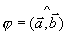 ,
, 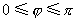 ,当
,当 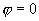 或
或 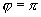 时,称为
时,称为  与
与 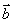 平行,记作
平行,记作 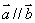 ,当
,当 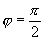 时称
时称  与
与 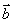 垂直记为
垂直记为 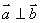 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com