1．若，则的值(　)

　　　 A．1　　　　　　　　　　　　　 B．-1　　　　　　　　　　　　　 C．0　　　　　　　　　　　　　 D．2

16．对于命题：如果是线段上一点，则；将它类比到平面 的情形是：若是△内一点，有；将它类比到空间的情形应该是：若是四面体内一点，则有 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　.

三　 解答题：本大题共6小题，共70分。接答应写出文字说明，证明过程或演算步骤。

17题(本小题满分10分)

在中，

(1)求的值；

(2)求的取值范围。

18题(本小题满分12分)

如图，已知三棱柱的侧棱与底面垂直，，且，是的中点，是的中点，点在直线上，

　 且满足。

　 (1)证明：；

　 (2)当取何值时，直线与平面所成的角

最大？并求该角最大值的正切值；

19题(本小题满分12分)

一学生参加某高校的自主招生考试，须依次参加A、B、C、D、E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试。已知每一项测试都是相互独立的，该生参加A、B、C、D四项考试不合格的概率均为，参加第五项不合格的概率为.

(1)求该生被录取的概率；

(2)记该生参加考试的项数为，求的分布列和期望.

20题(本小题满分12分)

已知向量\S\UP6(→＝(2，0)，O是坐标原点，动点 M 满足：| \S\UP6(→+ \S\UP6(→|+| \S\UP6(→－\S\UP6(→| ＝ 6。

　 (1)求点 M 的轨迹 C 的方程；

　 (2)是否存在直线 l 过 D(0，2)与轨迹 C 交于 P、Q 两点，且以 PQ 为直径的圆过原点，若存在，求出直线 l 的方程；若不存在，说明理由．

21题(本小题满分12分)

已知函数，其中为自然对数的底数，。

(1)设，求函数的最值；

(2)若对于任意的，都有成立，

求的取值范围。

选答题(本小题满分10分)(请考生在第22、23两道题中任选一题做答，并用2B铅笔在答题卡上把所选题目的题号涂黑。注意所做题号必须与所涂题目的题号一致，并在答题卡指定区域答题。如果多做，则按所做的第一题计分。)

22题(本小题满分10分)

选修4-1：几何证明选讲

⊙O如图：是内接于⊙O，AB=AC，直线MN切⊙O于点C，弦BD//MN，AC与BD相交于点E。

　　 ⑴求证：；

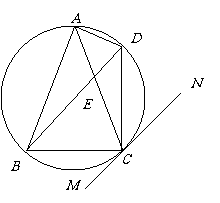　　 ⑵若AB=6，BC=4，求AE。

23题(本小题满分10分)

选修4-5：不等式选讲

设函数．

　 (Ⅰ)求不等式的解集；

(Ⅱ)若不等式的解集是非空的集合，求实数的取值范围．

14．若二项式的展开式中的常数项为-160，则=　　　　　　　　　　　　　　　　　　　　　　　　　　　　

13．已知函数，在区间［2，3］上任取一点＞0的概率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　

12．设均为大于1的正数，且，若的最小值为，则满足的整点的个数为(　　 )

A．5　　　　　　　　　　 B．7　　　　　　 C．9　　　　　　　 D．11

第Ⅱ卷(非选择题90分)

二　 填空题：本大题共4个小题，每小题5分，共20分。把答案填在横线上。

11．如果使得=，实数的关系为(　　 )

A．　　　　　 B．　　　 C．　　　　 D．

10.若实数满足不等式组目标函数的最大值为2，则实数的值是(　　 )

A．-2　　　　　　　　　 B．0　　 　　　　　C．1　　　　　　　 D．2

9.若把函数的图象向右平移(＞0)个单位长度后，所得到的图象关于轴对称，则的最小值是(　 )

　 A．　　　　　　　　　 B．　　　　　　 C．　　　　　　　 D．

8．已知双曲线的一个焦点与抛物线的焦点重合，且双曲线的离心率等于，则该双曲线的方程为(　　 )

　 A．　　　　 B.　　　 C.　　　　 D.

7．在△中，、、分别是三内角A、B、C的对边，且，则角C等于(　　 )

　 A．　　　　　　　　　 B．　　　 　　　　C．　　　　　　 D．